Denklem Sistemleri ve Eşitsizlikler
Birinci dereceden iki bilinmeyenli denklem sistemi a,b,c ∈ R ; a ve b sıfirdan farklı, x ve y değişkenler olmak üzere ax + by + c = 0 denklemi birinci dereceden iki bilinmeyenli denklemdir.
Birinci dereceden iki bilinmeyenli en az iki denklemin oluşturduğu sisteme birinci dereceden iki bilinmeyenli denklem sistemi denir. Örneğin: 3x + 8y = 7 ve 5x - 9y = 11 denklemlerinin oluşturduğu sistem birinci dereceden iki bilinmeyenli denklem sistemidir.
a,b,c,d,e,f ∈ R ve a,b,c reel sayılarından en az ikisi sıfırdan farklı olmak üzere ax2 + bxy + cy2 + dx + ey + f = 0 şeklindeki ifadelere ikinci dereceden iki bilinmeyenli bir denklem denir.
İki bilinmeyenli en az iki denklemden oluşan sistemin denklemlerinden en az biri ikinci dereceden denklem ise bu sisteme ikinci dereceden iki bilinmeyenli denklem sistemi denir. Denklemlerin ortak çözüm kümesi ( ÇK ) denklem sisteminin çözüm kümesidir.
Giriş
- İki değişkenli bir Doğrusal Denklem sistemi genellikle şu şekilde yazılır:
{ a1x+b1y=c1
a2x+b2y=c2
Bu aynı zamanda iki değişkenli eşzamanlı doğrusal denklemler olarak da adlandırılır. - (x,y) sayı çifti, sistemdeki denklemlerin doğru olmasını sağlayan çözüme denir.
- Aşağıda, iki değişkenli doğrusal sistemlere bazı örnekler verilmiştir:
{ 2x + y = 8
3x - y = 7,
{ y = x - 9
6x -6y = 54 ve
{ 4x - y = 5
4x - y = 1 - Tek bir sol köşeli parantez tipik olarak "ve" kelimesinin yerini alacak sistemleri belirtir.
- İki değişkendeki iki veya daha fazla doğrusal eşitsizlik, bir doğrusal eşitsizlikler sistemi oluşturur. Çözüm, sistemdeki her iki eşitsizliği de karşılayan sıralı bir çifttir.
- İki değişkenli doğrusal eşitsizlik, aşağıdaki biçimlerden herhangi biriyle ifade edilebilen bir eşitsizliktir:
{ a1x + b1y < c1
a2x + b2y > c2 veya
{ a1x + b1y ≤ c1
a2x + b2y ≥ c2
İki Değişkenli Doğrusal Sistem Türleri
Tutarlı Denklemler ( veya Bağımsız Denklemler ):
- Bunlar benzersiz bir çözümü olan denklem çiftleridir. Kesişme noktası (x,y), verilen denklem çiftinin çözümüdür.
- Standart formda yazılmış herhangi bir doğrusal denklem sistemi için
{ a1x + b1y = c1
a2x + b2y = c2, tutarlı denklemlerin bir formu vardır
a1/a2 ≠ b1/b2
Tutarsız Denklemler:
- Bunlar çözümü olmayan denklem kümeleridir. İki çözüm kümesinin kesişimi boş bir kümedir.
- Standart formda yazılmış herhangi bir doğrusal denklem sistemi için
{ a1x + b1y = c1
a2x + b2y = c2, tutarsız denklemlerin bir formu vardır
a1/a2 = b1/b2 ≠ c1/c2
Bağımlı Denklemler:
- Bunlar, sistemdeki sonsuz sayıda çözümü olan denklemlerdir. Bu iki doğrusal denklem tipik olarak eşdeğerdir.
- Standart formda yazılmış herhangi bir doğrusal denklem sistemi için
{ a1x + b1y = c1
a2x + b2y = c2, bağımlı denklemler formu takip eder
a1/a2 = b1/b2 = c1/c2
Eliminasyon ve ikame yöntemi kullanılarak çözülmüş örnekler
Örnek 1. Doğrusal sistemi çözün
{ 2x - 3y = -1
x + 3y = 4 Eliminasyon Yöntemini kullanarak.
Çözüm:
y'yi ortadan kaldırmak için iki denklem ekleyin.
(2x - 3y = -1) + (x + 3y = 4)
Bu oluşur 3x = 3 hangi verim x = 1. Y'nin değerini bulmak için elde edilen x değerini sistemdeki denklemlerden herhangi biriyle değiştirin.
2(1) -3y = -1
2 - 3y = -1
-3y = -3
y = 1
Böylece, sisteme çözümler x = 1 and y = 1.
Örnek 2. Doğrusal sistemi çözün
{ 3x + 4y = 2
y = x - 3 İkame Yöntemini kullanarak.
Çözüm:
Sahip olduğumuzdan beri y = x - 3, ifadenin yerine koyun (x - 3) içinde 3x + 4y = 2 x'i çözmek için.
3x + 4(x - 3) = 2
3x + 4x - 12 = 2
7x = 14
x = 2
Şimdi, yerine koyun x = 2 içinde y = x - 3.
y = 2 - 3 → y = -1
Doğrusal sistemin çözümleri şunlardır x = 2 ve y = -1.
Lineer Denklemlerin Grafik Sistemleri
- Doğrusal denklem sistemlerinin grafiğini çizmek için, x-kesişim noktası ve y-kesişim noktasını bulmamız gerekir. İki değişkenli doğrusal bir sistemin grafikleri, denklemlerin türünü ve çözümlerini belirler.
- Doğrusal sistem, iki çizgi bir noktada kesişirse tutarlı ve bağımsızdır.
- İki çizgi paralelse, doğrusal sistem tutarsızdır.
- Denklemler aynı grafiğe sahipse, doğrusal sistem bağımlıdır.
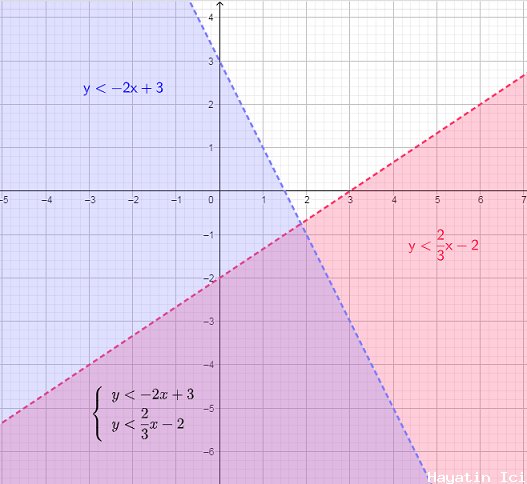
Doğrusal Eşitsizlikler Sistemi ve Grafikleri
- İki değişkenli doğrusal bir eşitsizliğin grafiği bir yarım düzlemdir. Eşitsizlik ise yarım düzlemin sınır çizgisi kesiklidir. < veya > ve eşitsizlik ise sağlam ≤ veya ≥.
- Sistemdeki her eşitsizliği aynı eksen kümesinde grafiklendirin.
- Çözüm kümesinin grafiği, grafiği çizilen bölgeler için ortak olan bölgedir.
- Çözüm kümesi içinde herhangi bir rastgele nokta seçin.
- Her iki ilişkiyi de karşılayıp karşılamadığını kontrol etmek için sıralı çifti orijinal eşitsizliklerle değiştirin.
İki Değişkenli Doğrusal Eşitsizliklerin Çözülmüş Örneği
Sistemin grafiğini çizin
{ x - y < 3
3x + y > 6
Çözüm:
Aşama 1. Grafiğini çizin x - y < 3. Grafik, çizginin üzerindeki açık yarım düzlemdir x - y = 3.
Adım 2. Aynı koordinat ızgarasını kullanarak, grafik 3x + y > 6. Grafik, çizginin üzerindeki açık yarım düzlemdir 3x + y = 6.
Sistemin grafiğinin çift gölgeli alan olduğuna dikkat edin.
Çift gölgeli bölgede bir nokta olan (2, 2) öğesini seçin.
Onu sistemdeki eşitsizliklerle değiştirin.
x - y < 3
2 - 2 < 3 → 0 < 3 ( DOĞRU )
3x + y > 6
3(2) + 2 > 6 → 8 > 6 ( DOĞRU )
Hile Sayfası
- Örnekte
{ 2x + 4y = -1
4x + 3y = 5, çözümü bulmak için sistemdeki denklemlerden birini veya her ikisini uygun bir sayı ile çarparız. Bu aynı zamanda bir tür eleme yöntemidir. - Sistemdeki denklemlerin eğimleri eşitse ve y-kesişim noktaları eşit değilse, doğrusal sistemin çözümü yoktur.
- Sistemdeki denklemlerin eğimleri eşit değilse ve y-kesişim noktaları eşit veya eşit değilse, doğrusal sistemin bir çözümü vardır.
- Sistemdeki denklemlerin hem eğimleri hem de y-kesişim noktaları eşitse, doğrusal sistemin sonsuz çözümü vardır.
- Sistemdeki çizgilerin eğimlerinin eşit olup olmadığını belirlemek için, denklemleri eğim-kesişim biçiminde değiştirebiliriz
{ y = m1x + b1
y = m2x + b2 - İki değişkenli veya eşitsizlikli doğrusal sistemleri içeren kelime problemlerini çözerken, problemi dikkatlice okuyun ve anlayın. Hangi miktarların bilinmediğine karar verin ve bunları sembollerle temsil edin. Verilen koşullara dayanarak, iki doğrusal model formüle edin. Sistemi cebirsel veya grafiksel olarak çözün. Verilen koşullara göre son cevaplarınızı kontrol edin. Doğrusal eşitsizlikler için, grafiğin çizilmesi her zaman gereklidir.
Blunder Alanları
- Cebirsel yöntemler kullanarak iki değişkenli doğrusal bir sistemi çözerken her zaman temel tamsayı işlemlerini kullanmaya dikkat edin.
- İki değişkenli tüm doğrusal denklem sistemleri standart biçimde yazılmamıştır
{ a1x + b1y = c1
a2x + b2y = c2 Bu gibi durumlarda, sistemdeki denklemleri her zaman standart formlarda veya eğim-kesişim formlarında basitleştirin. - X ve y'nin değerlerini bulduktan sonra, her zaman her iki denklemdeki değerleri de kontrol edin.
- Katı/saf eşitsizlik sembollerinin kullanımına dikkat edin < or > ve saf olmayan eşitsizlik sembolleri (≤ or ≥) İki değişkenli doğrusal eşitsizlik sisteminin çözümünü bulurken.
- Üç değişkenli doğrusal bir sistemi çözmek için eliminasyon ve ikame yöntemlerini hala kullanabiliriz. Bununla birlikte, matrisleri ve determinantları kullanmak daha uygundur.
- Doğrusal sistemdeki denklemler tarafından modellenen kesişen iki çizgi dik olabilir. Olup olmadığını görmek için eğimlerini inceleyin m1 = - 1/m2.