Basit Harmonik Hareket

BİLİM ve TEKNOLOJİ 23.10.2024 111 0

Bir gitar telini kopardığınızda, ortaya çıkan ses sabit bir tona sahiptir ve uzun süre devam eder ( Şekil-1 ). İp bir denge konumu etrafında titreşir ve ip başlangıç konumundan başladığında, en uç konumlardan birine, ardından diğer uç konuma hareket ettiğinde ve başlangıç konumuna geri döndüğünde bir salınım tamamlanır. Periyodik hareketi, gitar teli veya salıncakta sallanan bir çocuk tarafından sergilendiği gibi, düzenli zaman aralıklarında kendini tekrar eden herhangi bir hareket olarak tanımlarız. Bu bölümde, salınımların temel özelliklerini ve matematiksel tanımlarını inceliyoruz.

Şekil-1: Bir gitar teli koparıldığında, tel periyodik hareketle yukarı ve aşağı salınır. Titreşen ip, çevredeki hava moleküllerinin salınmasına ve ses dalgaları üretmesine neden olur

Salınımlarda Periyot ve Frekans

Sürtünmenin yokluğunda, bir salınımı tamamlama süresi sabit kalır ve periyot (T) olarak adlandırılır. Birimleri genellikle saniyedir, ancak herhangi bir uygun zaman birimi olabilir. 'Dönem' sözcüğü, yinelenen ya da yinelenmeyen, bir olayın zamanını ifade eder, ancak bu bölümde, öncelikle, tanımı gereği tekrarlayan olan periyodik hareketi ele alacağız. Dönemle yakından ilgili bir kavram, bir olayın sıklığıdır. Frekans (f), birim zamandaki olay sayısı olarak tanımlanır. Periyodik hareket için frekans, birim zamandaki salınım sayısıdır. Sıklık ve periyot arasındaki ilişki

f = 1/T ( Denklem-1 )

Frekans için SI birimi hertz'dir ( Hz ) ve saniyede bir döngü olarak tanımlanır:

1 Hz = 1cyde/sec veya 1 Hz = 1/s = 1 s⁻¹ ( Denklem-2 )

Bir döngü tam bir salınımdır.

Örnek-1: Medikal Ultrason Sıklığının Belirlenmesi

Ultrason makineleri, tıp uzmanları tarafından vücudun iç organlarını incelemek için görüntüler oluşturmak için kullanılır. Bir ultrason makinesi, organlardan yansıyan yüksek frekanslı ses dalgaları yayar ve bir bilgisayar, bir resim oluşturmak için kullanarak dalgaları alır. Salınımlar hakkında bildiklerimize dayanarak frekansı belirlemek için bu modülde sunulan formülleri kullanabiliriz. 0.400 periyot ile salınım yaparak ultrason üreten bir tıbbi görüntüleme cihazı düşünün μμs. Bu salınımın frekansı nedir?

Strateji

Periyot (T) verilir ve frekansı (f) bulmamız istenir.

Çözüm

f = 1/T'de T yerine 0,400 µs koyun:

f = 1/T = 1/0.400 × 10⁻⁶s

Bulmak için çöz,

f = 2,50 × 10⁶ Hz

Mana

Bu ses frekansı, insanların duyabileceği en yüksek frekanstan çok daha yüksektir ( insan işitmearalığı 20 Hz ila 20.000 Hz'dir ); Bu nedenle ultrason olarak adlandırılır. Bu frekanstaki uygun salınımlar, rahimdeki bir fetüsün gözlemleri gibi invaziv olmayan tıbbi teşhisler için kullanılan ultrason üretir.

Basit Harmonik Hareketin Özellikleri

Çok yaygın bir periyodik hareket türüne basit harmonik hareket ( SHM ) denir. SHM ile salınan bir sisteme basit harmonik osilatör denir.

Basit Harmonik Hareket

Basit harmonik harekette, sistemin ivmesi ve dolayısıyla net kuvvet, yer değiştirme ile orantılıdır ve yer değiştirmenin tersi yönünde hareket eder.

SHM'ye iyi bir örnek, kütlesi olan bir nesnedir mm Şekil-2'de gösterildiği gibi sürtünmesiz bir yüzey üzerinde bir yaya tutturulmuştur. Cisim denge konumu etrafında salınır ve cisim üzerindeki net kuvvet, yayın sağladığı kuvvete eşittir. Bu kuvvet Hooke'un F_s = −kx yasasına uyar, önceki bir bölümde tartışıldığı gibi. Net kuvvet Hooke yasası ile tanımlanabiliyorsa ve sönümleme ( sürtünme veya diğer korunumlu olmayan kuvvetler nedeniyle yavaşlama ) yoksa, o zaman basit bir harmonik osilatör, Şekil-2'de bir yay üzerindeki bir nesne için gösterildiği gibi, denge konumunun her iki tarafında eşit yer değiştirme ile salınır. Dengeden maksimum yer değiştirmeye genlik (A) denir. Genlik ve yer değiştirmebirimleri aynıdır ancak salınım tipine bağlıdır. Yay üzerindeki nesne için genlik ve yer değiştirmebirimleri metredir.

Şekil-2: - Sürtünmesiz bir yüzey üzerinde kayan bir yaya bağlı bir nesne, karmaşık olmayan basit bir harmonik osilatördür. Yukarıdaki şekil setinde, bir yaya bir kütle tutturulmuş ve sürtünmesiz bir masaya yerleştirilmiştir. Yayın diğer ucu duvara tutturulmuştur. Yay ne gerildiğinde ne de sıkıştırıldığında kütlenin konumu x = 0 olarak işaretlenir ve denge konumudur. (a) Kütle x = A konumuna yer değiştirir ve hareketsiz halden serbest bırakılır. (b) Kütle negatif x yönünde hareket ettikçe hızlanır ve x = 0'da maksimum negatif hıza ulaşır. (c) Kütle negatif x yönünde hareket etmeye devam eder ve x = -A'da durana kadar yavaşlar. (d) Kütle şimdi pozitif x yönünde hızlanmaya başlar ve x = 0'da pozitif bir maksimum hıza ulaşır. (e) Kütle daha sonra x = A'da durana kadar pozitif yönde hareket etmeye devam eder. Kütle, genliği A ve periyodu T olan SHM'de devam eder. Cismin maksimum hızı, dengeden geçerken meydana gelir. Yay ne kadar sert olursa, T periyodu o kadar küçük olur. Cismin kütlesi ne kadar büyükse, T periyodu o kadar büyük olur.

SHM hakkında bu kadar önemli olan nedir? Bir kere, dönem TT ve frekans ff basit bir harmonik osilatörün genliğinden bağımsızdır. Örneğin bir gitarın teli, ister nazikçe ister sert koparılsın, aynı frekansta salınır. Basit bir harmonik osilatörün periyodunu etkileyen iki önemli faktör vardır. Periyot, sistemin ne kadar sert olduğu ile ilgilidir. Çok sert bir cismin büyük bir kuvvet sabiti (k) vardır, bu da sistemin daha küçük bir periyoda sahip olmasına neden olur. Örneğin, bir dalış tahtasının sertliğini ayarlayabilirsiniz - ne kadar sert olursa, o kadar hızlı titreşir ve süresi o kadar kısa olur. Periyot ayrıca salınım yapan sistemin kütlesine de bağlıdır. Sistem ne kadar büyük olursa, süre o kadar uzun olur. Örneğin, bir dalış tahtası üzerindeki ağır bir kişi, hafif olandan daha yavaş yukarı ve aşağı zıplar. Aslında, kütle m ve kuvvet sabiti k, SHM'nin periyodunu ve frekansını etkileyen tek faktördür. Periyot ve frekans için bir denklem türetmek için önce hareket denklemlerini tanımlamalı ve analiz etmeliyiz. Kuvvet sabitinin bazen yay sabiti olarak adlandırıldığına dikkat edin.

SHM Denklemleri

Sürtünmesiz bir masa üzerinde bir yaya bağlı bir blok düşünün ( Şekil-3 ). Denge konumu ( yayın ne gerildiği ne de sıkıştırıldığı konum ) x = 0 olarak işaretlenir. Denge konumunda net kuvvet sıfırdır.

Yatay bir yaya bir blok tutturulur ve sürtünmesiz bir masaya yerleştirilir.

Şekil-3: Bir yaya bir blok tutturulur ve sürtünmesiz bir masaya yerleştirilir. Yayın ne uzatıldığı ne de sıkıştırıldığı denge konumu x = 0 olarak işaretlenir.

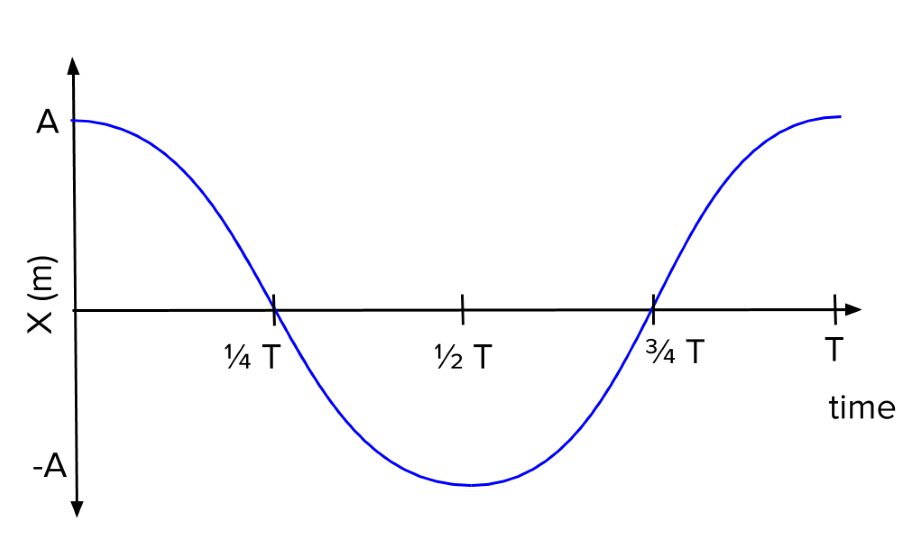
Blok üzerinde x = + A konumuna çekmek için çalışma yapılır ve daha sonra dinlenmeden serbest bırakılır. Maksimum x konumuna (A) hareketin genliği denir. Blok, SHM'de x = + A ve x = −A arasında salınmaya başlar, burada A hareketin genliği ve T salınım periyodudur. Periyot, bir salınım zamanıdır. Şekil-4 Serbest bırakıldıktan sonra bir buçuk salınımı tamamlarken bloğun hareketini gösterir.

Yatay bir yaya tutturulmuş ve yatay bir yüzey üzerinde kayan bir kütlenin bir dizi çizimi gösterilmektedir

Şekil-4: Bir yayın bir ucuna bir blok takılır ve sürtünmesiz bir masaya yerleştirilir. Yayın diğer ucu duvara sabitlenmiştir. Net kuvvetin sıfıra eşit olduğu denge konumu x = 0 m olarak işaretlenir. Blok üzerinde çalışma yapılır, x = + A'ya çekilir ve blok dinlenmeden serbest bırakılır. Blok x = + A ve x = -A arasında salınır. Kuvvet aynı zamanda bir vektör olarak da gösterilir.

Şekil-4 Bloğun zamana karşı konumunun bir grafiğini gösterir. Konum zamana karşı çizildiğinde, verilerin genlikli bir kosinüs fonksiyonu tarafından modellenebileceği açıktır A ve bir dönem T. Kosinüs fonksiyonu cosθ 2π'nin her katını tekrarlar, oysa bloğun hareketi her T periyodunda bir tekrar eder. Ancak, işlev cos(2π/T t) Dönemin her tamsayı katını tekrarlar. Kosinüs fonksiyonunun maksimumu birdir, bu nedenle kosinüs fonksiyonunu A genliği ile çarpmak gerekir.

x(t) = Acos(2π/T t) = Acos(ωt) ( Denklem-3 )

Dönme ile ilgili bölümden açısal frekansın eşit olduğunu hatırlayın ω = dθ/dt. Bu durumda, periyot sabittir, bu nedenle açısal frekans 2π olarak tanımlanır döneme bölünmüş, ω = 2π/T.

Yatay eksende zamanın bir fonksiyonu olarak dikey eksen üzerindeki konumun grafiği

Şekil-5: Şekilde gösterilen bloğun konumunun bir grafiği zamanın bir fonksiyonu olarak. Konum, kosinüs veya sinüs fonksiyonu gibi periyodik bir fonksiyon olarak modellenebilir.

Zamanın bir fonksiyonu olarak konum denklemi x(t) = Acos(ωt) bloğun başlangıç zamanındaki t = 0.00 s konumunun A genliğinde ve ilk hızın sıfır olduğu verileri modellemek için iyidir. Genellikle deneysel veriler alınırken, kütlenin ilk zaman t = 0.00 s'deki konumu genliğe eşit değildir ve ilk hız sıfır değildir. Şekil-6'da gösterildiği gibi, bir öğrenci tarafından laboratuvarda toplanan 10 saniyelik verileri düşünün.

Bir yay üzerindeki bir kütle için zamana karşı konum verileri

Şekil-6: Laboratuvarda bir öğrenci tarafından toplanan veriler, sonik bir telemetre ile ölçülen bir yaya bağlı bir bloğun konumunu gösterir. Veriler t = 0.00s zamanından başlayarak toplanır, ancak başlangıç konumu x konumuna ≈ - 0.80 cm ≠ 3.00 cm yakındır, bu nedenle başlangıç konumu x genliğine eşit değildir0 = + A'dır. Hız, konuma karşı zaman grafiğindeki bir noktadaki eğim olan konumun zaman türevidir. Hız, t = 0.00 s zamanında v = 0.00 m/s değildir, konuma karşı zaman grafiğinin eğimi ile gösterildiği gibi, başlangıçta sıfır değildir.

Şekil-6'daki veriler yine de kosinüs fonksiyonu gibi periyodik bir fonksiyonla modellenebilir, ancak fonksiyon sağa kaydırılır. Bu kayma faz kayması olarak bilinir ve genellikle Yunanca phi (φ) harfi ile temsil edilir. Bir yay üzerindeki bir blok için zamanın bir fonksiyonu olarak konumun denklemi şu hale gelir:

x(t) = Acos(ωt + φ) ( Denklem-4 )

Bu, SHM için genelleştirilmiş denklemdir, burada t saniye cinsinden ölçülen zamandır, ω ters saniye birimlerine sahip açısal frekanstır, A, metre veya santimetre cinsinden ölçülen genliktir ve φ radyan cinsinden ölçülen faz kaymasıdır ( Şekil-7 ). Sinüs ve kosinüs fonksiyonları sadece bir faz kayması ile farklılık gösterdiğinden, bu hareketin kosinüs veya sinüs fonksiyonu kullanılarak modellenebileceğine dikkat edilmelidir.

Şekil-7: (a) Bir kosinüs fonksiyonu. (b) Bir açı ile sağa kaydırılan bir kosinüs fonksiyonu φφ. Açı φφ fonksiyonun faz kayması olarak bilinir.

SHM'de salınan bir yay üzerindeki kütlenin hızı, konum denkleminin türevi alınarak bulunabilir:

v(t) = dx/dt = d/dt (Acos(ωt + φ)) = -Aωsin(ωt + φ) = -v_maxsin(ωt + φ) ( Denklem-5)

Sinüs fonksiyonu –1 ile +1 arasında salındığından, maksimum hız, genlik çarpı açısal frekans, v_max = Aω. Maksimum hız, kütle x = + A'ya doğru hareket ederken denge konumunda (x = 0) meydana gelir. Negatif yöndeki maksimum hız, kütle x = −A'ya doğru hareket ederken ve −v_max'ye eşit olduğunda denge konumunda (x = 0) elde edilir. Yay üzerindeki kütlenin ivmesi, hızın zaman türevi alınarak bulunabilir:

a(t) = dv/dt = d/dt (−Aωsin(ωt + φ)) = -Aω² cos(ωt + φ) = -a_maxcos(ωt + φ) ( Denklem-6)

Maksimum hızlanma a_max = Aω². Maksimum ivme (x = -A) konumunda ve ivme (x = -A) konumunda meydana gelir ve -a_max'ya eşittir.

SHM için Hareket Denklemlerinin Özeti

Özetle, bir bloğun bir yay üzerindeki salınım hareketi aşağıdaki hareket denklemleri ile modellenebilir:

x(t) = Acos(ωt + φ) ( Denklem-7)

v(t) = −v_max sin⁡(ωt + φ) ( Denklem-8)

a(t) = −a_max cos⁡(ωt + φ) ( Denklem-9)

ile

x_max = A ( Denklem-10)

v_max = Aω ( Denklem-11)

a_max = Aω² ( Denklem-12)

Burada A hareketin genliğidir, T dönemdir, φ faz kaymasıdır ve ω = 2π/T = 2πf, bloğun hareketinin açısal frekansıdır.

Örnek-2: Bir Blok ve Bir Yay için Hareket Denklemlerinin Belirlenmesi

Sürtünmesiz bir yüzeye 2,00 kg'lık bir blok yerleştirilir. Bloğa k = 32.00 N/m kuvvet sabiti olan bir yay tutturulur ve yayın karşı ucu duvara tutturulur. Yay sıkıştırılabilir veya uzatılabilir. Denge konumu x = 0.00 m olarak işaretlenmiştir. Blok üzerinde çalışma yapılır, x = + 0.02 m'ye çekilir. Blok dinlenmeden serbest bırakılır ve x = + 0.02 m ile x = -0.02 m arasında salınır. Hareketin süresi 1.57 sn'dir. Hareket denklemlerini belirleyin.

Strateji

Önce açısal frekansı buluyoruz. Faz kayması sıfırdır, φ = 0.00 rad, çünkü blok x = A = + 0.02 m'de dinlenmeden serbest bırakılır. Açısal frekans bulunduğunda, maksimum hızı ve maksimum ivmeyi belirleyebiliriz.

Çözüm

Açısal frekans, maksimum hızı ve maksimum ivmeyi bulmak için bulunabilir ve kullanılabilir:

ω = 2π/1.57s = 4.00 s⁻¹ ;

v_max = Aω = (0.02 m)(4.00 s⁻¹) = 0.08 m/s ;

a_max = Aω² = (0.02; m)(4.00 s⁻¹)² = 0.32 m/s² .

Geriye kalan tek şey hareket denklemlerini doldurmak:

x(t) = a cos(ωt + φ) = (0.02 m) cos(4.00 s⁻¹t) ;

v(t) = −v_max sin(ωt + φ) = (−0.8 m/s) sin⁡(4.00 s⁻¹t) ;

a(t) = −a_max cos(ωt + φ) = (−0.32 m/s²) cos⁡(4.00 s⁻¹t) .

Mana

Konum, hız ve ivme herhangi bir zaman için bulunabilir. Bu denklemleri kullanırken hesap makinenizin radyan modunda olması gerektiğini unutmamak önemlidir.

Bir yay üzerindeki bir kütlenin periyodu ve frekansı

Bir yaya bağlı bir cismin SHM'sinin ilginç bir özelliği, açısal frekansın ve dolayısıyla hareketin periyodu ve frekansının, hareketin genliği gibi diğer faktörlere değil, yalnızca kütleye ve kuvvet sabitine bağlı olmasıdır. Hareket denklemlerini ve Newton'unikinciyasasını kullanabiliriz ( F→_net = ma→ ) açısal frekans, frekans ve periyot denklemlerini bulmak için. Sürtünmesiz bir yüzeydeki bir yay üzerindeki bloğu düşünün. Kütle üzerinde üç kuvvet vardır: ağırlık, normal kuvvet ve yaydan kaynaklanan kuvvet. Yüzeye dik olarak etki eden tek iki kuvvet, eşit büyüklüklere ve zıt yönlere sahip olan ağırlık ve normal kuvvettir ve bu nedenle toplamı sıfırdır. Yüzeye paralel hareket eden tek kuvvet, yaydan kaynaklanan kuvvettir, bu nedenle net kuvvet, yayın kuvvetine eşit olmalıdır:

F_χ = −kχ ;

ma = −kχ ;

m d²χ/dt² = −kχ .

d²χ/dt² = − k/m χ .

x ve a için hareket denklemlerini yerine koymak bize şunu verir:

-Aω² cos(ωt + φ) = - k/m Acos(ωt + φ) ( Denklem-13)

Benzer terimleri iptal etmek ve açısal frekans verimlerini çözmek,

ω = √k/m ( Denklem-14 )

Açısal frekans, genliğe değil, yalnızca kuvvet sabitine ve kütleye bağlıdır. Açısal frekans şu şekilde tanımlanır: ω = 2π/T , bu da hareketin periyodu için bir denklem verir:

T = 2π√m/k ( Denklem-15 )

Periyot ayrıca sadece kütleye ve kuvvet sabitine bağlıdır. Kütle ne kadar büyükse, süre o kadar uzun olur. Yay ne kadar sert olursa, süre o kadar kısa olur. Frekans,

f = 1/T = 1/2π √k/m ( Denklem-16 )

Dikey Hareket ve Yatay Yay

Bir yay dikey olarak asıldığında ve bir blok takılıp harekete geçirildiğinde, blok SHM'de salınır. Bu durumda normal bir kuvvet yoktur ve yerçekimi kuvvetinin net etkisi denge konumunu değiştirmektir. Şekil-8'i Düşünün Bloğa iki kuvvet etki eder: yayın ağırlığı ve kuvveti. Ağırlık sabittir ve yayın uzunluğu değiştikçe yayın kuvveti de değişir.

Tavana tutturulmuş dikey bir yayın bir çizimi

Şekil-8: Tavandan bir yay asılır. Bir blok takıldığında, blok, bloğun ağırlığının yayın kuvvetine eşit olduğu denge konumundadır. (a) Yay tavana asılır ve denge konumu yo olarak işaretlenir. (b) Yaya bir kütle bağlanır ve yeni bir denge konumuna ulaşılır ( y1 = y0 − ΔΔy ) Yay tarafından sağlanan kuvvet kütlenin ağırlığına eşit olduğunda. (c) Kütlenin serbest cisim diyagramı, kütleye etki eden iki kuvveti gösterir: yayın ağırlığı ve kuvveti.

Blok, Şekil-8 de görüldüğü gibi denge konumuna ulaştığında, yayın kuvveti bloğun ağırlığına eşittir, F_net = F_s - mg = 0, burada,

-k(−Δy) = mg ( Denklem-17 )

Şekilden, pozisyondaki değişiklik Δy = y₀ − y₁ ve o zamandan beri -k(−Δy) = mg yaptık,

k(y₀ − y₁) − mg = 0 ( Denklem-18 )

Blok yer değiştirir ve serbest bırakılırsa, yeni denge konumu etrafında salınacaktır. Şekil-9'da gösterildiği gibi, bloğun konumu zamanın bir fonksiyonu olarak kaydedilirse, kayıt periyodik bir fonksiyondur. Blok bir y konumuna yer değiştirirse, net kuvvet F_net = k(y₀ - y) - mg. Ancak denge konumunda mg = kΔy = ky₀ - ky₁ olduğunu bulduk. Denklemdeki ağırlığın yerine konması şu sonuçları verir,

F_net = ky₀ - ky − (ky₀ - ky₁) = k(y₁ − y) ( Denklem-19 )

Hatırla ki y₁ sadece denge konumudur ve herhangi bir konum y = 0.00 m noktası olacak şekilde ayarlanabilir. Öyleyse y₁'i ayarlayalım y = 0.00 m'ye kadar. kuvvet daha sonra olur,

F_net = -ky ;

m d²y/dt² = −ky .

Bu, daha önce bir yay üzerinde yatay olarak kayan bir kütle için bulduğumuz şeydi. Sabit yerçekimi kuvveti, yalnızca kütlenin denge konumunu değiştirmeye hizmet etti. Bu nedenle, çözelti yatay bir yay üzerindeki bir blokla aynı formda olmalıdır, y(t) = Acos(ωt + φ). Hız ve ivme denklemleri de yatay durum ile aynı forma sahiptir. Faz kaymasının dahil edilmesinin, hareketin aslında bir kosinüs veya bir sinüs fonksiyonu kullanılarak modellenebileceği anlamına geldiğine dikkat edin, çünkü bu iki fonksiyon yalnızca bir faz kayması ile farklılık gösterir.

Şekil-9: Dikey bir yaya tutturulmuş bir topun 10 çiziminden oluşan bir dizi gösterilmektedir. Çizimler, yayların üst kısımları hizalı olarak yan yana görüntülenir. y = + A, y = 0 ve y = -A dikey konumları sağda etiketlenmiştir. Soldan sağa doğru ilerliyoruz: En soldaki çizimde, yay sıkıştırılır, böylece top y = + A'da ve hareketsiz durumda olur. İkinci çizimde top y = 0'dadır ve aşağı doğru hareket etmektedir. Üçüncü çizimde, yay, top y = - A konumunda ve hareketsiz olacak şekilde gerilir. Dördüncü çizimde top y = 0'dır ve yukarı doğru hareket etmektedir. Beşinci çizimde, yay sıkıştırılır, böylece top y = + A'da ve hareketsiz olur. Altıncı çizimde top y = 0'dır ve aşağı doğru hareket etmektedir. Yedinci çizimde, yay, top y = - A'da ve hareketsiz olacak şekilde gerilir. Sekizinci çizimde top y = 0'dadır ve yukarı doğru hareket etmektedir. Dokuzuncu çizimde, yay sıkıştırılır, böylece top y = + A'da ve hareketsiz olur. Onuncu çizimde top y = 0'dadır ve aşağı doğru hareket etmektedir. Bu çizimlerin altında dikey olarak hizalanmış bir dizi grafik bulunmaktadır. Üstteki grafik, zamanın bir fonksiyonu olarak konumdadır. Dikey eksen, – A ila +A aralığında y konumudur. Yatay eksen, T'nin artışlarıyla etiketlenmiş t zamanıdır. Grafik, t=0'da y=+A değerine sahiptir ve iki ve bir çeyrek döngü salınır. Maksimumlar arasındaki yatay mesafe T olarak etiketlenir ve yatay eksen ile maksimum arasındaki dikey mesafe genlik A olarak etiketlenir. Ortadaki grafik, zamanın bir fonksiyonu olarak hıza aittir. Dikey eksen, eksi v alt maks ila v maks aralığında v hızıdır. Yatay eksen, T'nin artışlarıyla etiketlenmiş t zamanıdır. Grafiğin v=0 değeri ve t=0'da negatif bir eğimi vardır ve iki ve bir çeyrek döngü salınır. Alttaki grafik, zamanın bir fonksiyonu olarak ivmedir. Dikey eksen, eksi bir alt maks ile maksimum arasında bir aralıkta a ivmesidir. Yatay eksen, T'nin artışlarıyla etiketlenmiş t zamanıdır. Grafiğin a değeri eksi a, alt maks ve a'ya eşittir ve iki ve bir çeyrek döngüyü salınır. Grafiklerin altında, yay üzerindeki topun üç resmi bulunmaktadır. y = + A, y=0 ve y = -A konumları sağda etiketlenmiştir. En soldaki diyagramda, bir el topu tutar ve yayın uzunluğu gerilmemiş uzunluk olarak etiketlenir. Bu konum y = + A konumunun üzerindedir. Ortadaki resimde, top tutulmuyor ve denge konumu olarak etiketlenmiş daha düşük bir konumda. Bu konum y = 0'dır. En sağdaki diyagramda, top dört farklı pozisyonda gösterilmiştir. Bu pozisyonlar y = + A, y = 0'ın hemen üstünde, y = 0'ın hemen altında ve y = -A'da. Yay sadece alt kısmı y = + A konumunda bilyeye bağlı olarak gösterilir.

Şekil-10: Bir cismin dikey bir yay üzerindeki hareketi için y(t), v(t) ve a(t)'nin t'ye karşı grafikleri. Cisim üzerindeki net kuvvet Hooke yasası ile tanımlanabilir, bu nedenle cisim SHM'ye maruz kalır. Başlangıç konumunun maksimum değeri A'da dikey yer değiştirmeye sahip olduğuna dikkat edin; v başlangıçta sıfırdır ve daha sonra nesne aşağı hareket ettikçe negatiftir; İlk ivme negatiftir, denge konumuna geri döner ve bu noktada sıfır olur.