Açısal Momentum Nedir?

    Açısal Momentum, bir veya daha fazla nokta kütlesine sahip bir sistemin kinematik bir özelliğidir. Açısal momentum bazen doğrusal momentumun dönme eşdeğeri olan Dönme Momentumu veya Momentum Momenti olarak adlandırılır. Kapalı bir sistem için korunduğu ve Açısal Momentumun Korunumu Yasasını takip ettiği için önemli bir fiziksel niceliktir. Açısal Momentum, dönme hareketindeki bir cismin atalet momenti ( I ) ve açısal hızının ( ω ) çarpımına eşittir. Açısal Momentum bir vektör miktarıdır. Açısal momentumun SI birimi Kg.m².s^-1 'dir

    Açısal momentum hakkında daha fazla kavramı anlayalım, örneğin Açısal Momentum nedir? Açısal Momentum Formülü, Açısal Momentumun Birim ve Boyut Formülü, Spin ve Orbital Açısal Momentum, Tork ve Açısal Momentum Arasındaki İlişki, Açısal Momentumun Korunumu Yasası, SSS ve Açısal Momentum Örnekleri.

Açısal Momentum Nedir?

    Açısal Momentum, eylemsizlik momentleri ve açısal hızlarının çarpımı tarafından belirlenen dönme hareketindeki nesnelerin özelliği olarak tanımlanır.

    Bir parçacık sistemine hiçbir dış kuvvet etki etmediğinde, sistemdeki açısal momentumun korunduğu bulunur. Herhangi bir bileşik sistemin toplam açısal momentumu, bileşen elemanlarının her birinin açısal momentumunun toplamına eşittir ve bu da açısal momentumu geniş bir miktar yapar. Sürekli bir rijit cisim veya akışkan için toplam açısal momentum , açısal momentum yoğunluğunun hacim integralidir ( hacim sıfıra düştüğünde sınırdaki birim hacim başına açısal momentum ).

    Dünyanın dönüşü ve dönüşü, açısal momentumun en iyi örneklerinden birini verir. Örneğin, Dünya'nın kendi ekseni etrafındaki günlük dönüşü dönüş açısal momentumunu temsil ederken, Güneş etrafındaki yıllık dönüşü yörüngesel açısal momentumu temsil eder.

Açısal Momentum Formülü

    Dönme hareketindeki bir cismin açısal momentumu iki şekilde gerçekleşebilir.

Tek Bir Parçacığın Açısal Momentumu

    Açısal momentum, nesne sabit bir konum etrafında hızlanırken tek bir parçacık tarafından deneyimlenebilir. Örneğin, dünya ve güneş söz konusu olduğunda. Dünya, güneşin konumunda sabit olduğu yörüngesinde güneşin etrafında dönüyor.

    Açısal momentum, bu durumda aşağıdaki formülle verilir:

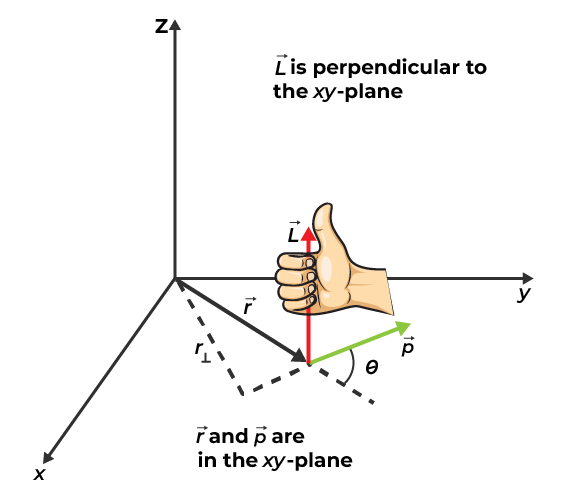
L^→ = r x p^→

    nerede

L^→

r, Dönme Yolunun Yarıçapıdır

p^→

Genişletilmiş Nesne için Açısal Momentum

    Açısal momentum, bir nokta cisim tarafından sabit bir konum etrafında dönerken deneyimlenebilir. Örneğin, dünyanın kendi ekseni etrafında dönmesi durumunda.

    Açısal Momentum, bu durumda aşağıdaki formülle verilir:

L^→ = I x ω^→

    nerede

L^→

I Dönme Ataletidir

ω^→

Bir parçacık sisteminin açısal momentumu

    Bir parçacık sisteminin Açısal Momentumu, tek parçacıkların tüm bireysel açısal momentumlarının vektörel toplamıdır. Herhangi bir parçacığın açısal momentumu, l = r×p burada r, parçacık formunun kökeninin mesafesidir. ve p, parçacığın doğrusal momentumudur. n parçacıklı sistemin açısal momentumu,

L = l₁ + l₂ + l₃ +...+ l_n

Rijit Bir Cismin Açısal Momentumu

    Cismin N kütleli parçacıklardan oluştuğunu varsayalım. m₁, m₂,....m_N ve dönme ekseninden r₁, r₂,....r_N dik uzaklıklar. Nesne dönerken, bu parçacıkların tümü UCM'yi aynı açısal hız ω ile ancak farklı çizgi hızları v₁ = r₁Ω, V₂ = r₂ω, ... v_N = r_Nω ile iletir.

    Bireysel hız yönleri, v₁, v₂ ve benzeri, kendi izlerinin teğetleri boyuncadır. İlk parçacığın doğrusal momentumudur. p₁ = m₁v₁ = m₁r₁ω. v₁ ile aynı yönde hareket eder. 

    Açısal momentumunun büyüklüğü sonuç olarak L₁ = p₁r₁ = m₁r₁²ω'dir. Benzer şekilde, L₂ = m₂r₂²ω, L₃ = m₃r₃²ω, … L_N = m_Nr_N²ω.

    Bu açısal momentumların tümü, sağ el başparmak kuralı kullanılarak belirlenebilen, sabit bir dönme eksenine sahip katı bir cisim için dönme ekseni boyunca yönlendirilir. Büyüklükleri cebirsel olarak toplanabilir çünkü hepsi aynı yöne sahiptir. Sonuç olarak, cismin açısal momentumunun büyüklüğü şu şekilde verilir:

L = m₁r₁²ω + m₂r₂²ω +....+ m_Nr_N²ω

∴ L = (m₁r₁² + m₂r₂² +...+ m_Nr_N²)ω = Iω

    Böylece, herhangi bir katı cismin açısal momentumu, 

L = Iω

Açısal Momentum Birimi

• Açısal Momentumun SI birimi kg.m²/s 'dir.
• Açısal Momentumun CGS birimi g.cm²/s 'dir.
• Açısal Momentum için boyutsal formül, [ML²T^-1].

Sağ El Başparmak Kuralı

    Açısal momentumun yönü sağ el başparmak kuralı ile belirlenebilir. Sağ elinizi, parmaklarınız r yönünü gösterecek şekilde konumlandırırsanız. Kıvrılma böylece doğrusal momentum ( p ) yönünde yönlendirilir. Uzatılmış başparmak, açısal momentumun ( L ) yönünü gösterir.

Açısal Momentum Kuantum Sayısı

    Azimut kuantum sayısı veya ikincil kuantum sayısı, açısal momentum kuantum sayısı ile değiştirilebilir. Bir atomik orbitalin açısal momentumunun yanı sıra boyutunu ve biçimini belirleyen bir kuantum sayısıdır. En yaygın değer 0 ile 1 arasındadır.

Açısal Momentum ve Atalet Momenti

    Cismin m₁, m₂,....m_N kütleli ve dönme ekseninden r₁, r₂,....r_N dik mesafeli N parçacıktan oluştuğunu varsayalım. Cisim dönerken, bu parçacıkların hepsi ω açısal hızıyla Düzgün Dairesel Hareket içindedir, ancak doğrusal hızları şöyledir,

• v₁ = r₁ω
• v₂ = r₂ω
• v_N = r_Nω

    Bireysel hız yönleri, v₁, v₂ ve benzeri, kendi izlerinin teğetleri boyuncadır. İlk parçacığın doğrusal momentumu p₁ = m₁v₁ = m₁r₁ω 'dır. v₁ ile aynı yönde hareket eder. 

    Açısal momentumunun büyüklüğü, L₁ = p₁r₁ = m₁r₁²ω

    Benzer şekilde, L₂ = m₂r₂²ω, L₃ = m₃r₃²ω, … L_N = m_Nr_N²ω

    Bu açısal momentumların tümü, sağ el başparmak kuralı kullanılarak belirlenebilen, sabit bir dönme eksenine sahip katı bir cisim için dönme ekseni boyunca yönlendirilir. Büyüklükleri cebirsel olarak toplanabilir çünkü hepsi aynı yöne sahiptir. Sonuç olarak, cismin açısal momentumunun büyüklüğü şu şekilde verilir:

L = m₁r₁²ω + m₂r₂²ω +....+ m_Nr_N²ω

L = (m₁r₁² + m₂r₂² +...+ m_Nr_N²)ω = Iω

    Verilen dönme ekseni etrafındaki cismin eylemsizlik momenti,

• I = m₁r₁² + m₂r₂² +...+ m_Nr_N²

    Eylemsizlik momenti I kütlenin yerini alırsa, açısal momentum ifadesi L = Iω, fiziksel önemi olan doğrusal momentum ifadesi p = mv ile karşılaştırılabilir.

Açısal Momentum Örnekleri

    Açısal Momentum kavramının olduğu çeşitli örnekler,

Jiroskop

    Yönünü korumak için, bir jiroskop açısal momentum ilkesini kullanır. Üç serbestlik dereceli çıkrık ile çalışır. Hızlı bir şekilde döndürüldüğünde yöne kilitlenir ve ondan sapmaz. Bu, bir uzay aracının tutumunu kontrol etmenin kritik olduğu uzay uygulamalarında kullanışlıdır.

Buz patencisi

    Buz patencileri bir tur atmaya başladıklarında, elleri ve bacakları vücutlarının merkezinden geniş bir şekilde yayılır. Eğirme daha yüksek bir açısal hız gerektirdiğinde ellerini ve bacaklarını vücutlarına yaklaştırırlar. Açısal momentumun korunumunun bir sonucu olarak daha hızlı dönerler.

Açısal Momentumun Korunumu Yasası

    Herkes, harici bir dengesiz kuvvetin yokluğunda, izole edilmiş bir sistemin doğrusal momentumunun korunduğunu belirten doğrusal momentumun korunumunu görmüştür. Dönme dinamiğinde, tork ve açısal momentum, daha önce belirtildiği gibi kuvvet ve doğrusal momentuma benzer. Doğru modifikasyonlarla bu, açısal momentum korunumuna dönüştürülebilir.

    Açısal momentum aşağıdaki formülle verilir,

L = r × p

    Nerede

• r, Dönme Ekseninden Konum Vektörüdür
• p Doğrusal Momentumdur

    Zamana göre farklılaşan,

    dL/dt = d/dt(r × p)

    dL/dt = r × (dp/dt) + (dr/dt) × p... (i)

    Şimdi

    (dr/dt) = v ve (dp/dt) = F

    Başlangıç eq(i)

    dL/dt =  r × F + m(v × v)

    Şimdi, (v × v) = 0

    ∴ dL/dt = r × F

    Ancak, r × F = τ

    ∴ τ = dL/dt

    Böylece, τ = 0 ise, dL/dt = 0 veya L = sabit

    Sonuç olarak, eşit olmayan dış tork τ yokluğunda, açısal momentum L korunur. Bu, doğrusal momentum korunumuna benzer olan açısal momentum korunumu ilkesidir.

Tork Nedir?

    Bir cismin bir eksen boyunca dönmesine neden olabilecek kuvvet tork ile ölçülür. Doğrusal kinematikte kuvvet, bir cismi ileri iten şeydir. Açısal bir ivme de torktan kaynaklanır. Sonuç olarak, tork, doğrusal kuvvetin dönen eşdeğeri olarak düşünülebilir. Dönme ekseni, bir nesnenin etrafında döndüğü noktadır. Tork, fizikte bir kuvvetin dönme veya bükülme eğilimi olarak tanımlanır.

    Tork Formülü,

τ = r × F

    nerede

• r Dik Uzaklıktır
• F, Cisme Uygulanan Kuvvettir

Hatırlanması Gereken Noktalar

• Açısal Momentum, atalet momenti ve açısal hızın çarpımı tarafından belirlenen herhangi bir dönen nesnenin niteliği olarak tanımlanır.
• 'L' açısal momentumunun büyüklüğü aşağıdaki formül kullanılarak hesaplanabilir: L = rmv sin Φ
• Spin ve yörünge açısal momentumu, iki tür açısal momentumdur.
• L = r × p, bir nokta nesnesinin açısal momentumunu hesaplamak için kullanılan formüldür.
• L = I × ω, uzun bir nesnenin açısal momentumunu hesaplamak için kullanılan formüldür.
• Çember Yarıçapı, tork uygulanmadığında bir cismin dik hızını belirler.

Sıkça Sorulan Sorular

1. Açısal Momentum Nedir?

    Açısal momentum, herhangi bir Dönen Cismin Atalet Momenti ve Açısal Hızının çarpımı olarak tanımlanır.

2. Açısal Momentumun Korunumu İlkesi Nedir?

    Açısal momentumun korunumu yasasına göre, sisteme etki eden hiçbir dış tork olmadığında, nesnenin açısal momentumu her zaman korunur.

3. Açısal Momentum Skaler mi yoksa Vektörel Büyüklük mü?

    Açısal Momentumun hem büyüklüğü hem de yönü vardır, bu nedenle bir Vektör Miktarıdır.

4. Açısal Momentum Kuantum Sayısı Nedir?

    Azimut kuantum sayısı veya ikincil kuantum sayısı, açısal momentum kuantum sayısı ile değiştirilebilir. Bir atomik orbitalin açısal momentumunun yanı sıra boyutunu ve biçimini belirleyen bir kuantum sayısıdır. En yaygın değer 0 ile 1 arasındadır.

5. Açısal Momentum ve Atalet Momenti Nedir?

    Herhangi bir cismin Açısal Momentumu, bir cismin Eylemsizlik Momenti ile Angualr Hızının çarpımıdır. Oysa Atalet Momenti ( MOI ), cismin kütlesinin dönme ekseni etrafında nasıl dağıldığının ölçüsüdür.

6. Açısal Momentum Her Zaman Korunur mu?

    Hayır, Açısal momentum yalnızca dönen gövdeye net dış tork uygulanmadığında korunur.