L'Hôpital Kuralı

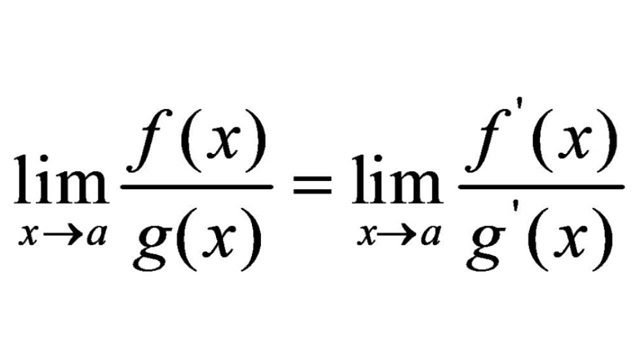
    L'Hôpital kuralı, belirli belirsiz form türlerinin sınırını bulmak için kullanılan bir teoremdir; Belirsiz formlar, ikame kullanımı yoluyla bir sınır hesaplama girişiminden kaynaklanan ifadelerdir. Örneğin, sınırları 0/0 veya ∞/∞ olarak değerlendirilen rasyonel fonksiyonlar, ifade limiti değerlendirmek için yeterli bilgi sağlamadığından belirsiz formlar olarak adlandırılır. Diğer belirsiz formlar şunları içerir: 0 · ±∞, ∞ - ∞, 1^∞, 0⁰ ve ∞⁰.

    Belirsiz formlar, hangi terimin baskın olduğunu belirsiz kılan rekabet eden kuralların olduğu bir ifadedeki terimler arasındaki bir yarışma olarak düşünülebilir; Bu, daha fazla inceleme yapılmadan işlevin sınırının ne olduğunu belirsiz hale getirir. Limitleri değerlendirmenin birkaç farklı yolu vardır. L'Hôpital kuralı yalnızca bir limitin belirsiz 0/0 veya ∞/∞ biçiminde olduğu ve limitin diğer yöntemler kullanılarak hesaplanamadığı durumlarda kullanılır.

    L'Hôpital kuralı aşağıdaki gibidir: Eğer f ve g türevlenebilir ise ve g'(x) ≠ 0 a içeren açık bir aralıkta ( muhtemelen a hariç ) ve aşağıdakilerden biri doğruysa,

1.   lim ƒ(x) = 0
     x→a
     ve
     lim g(x) = 0
     x→a




2.   lim ƒ(x) = ±∞
     x→a
     ve
     lim g(x) = ±∞
     x→a

    sonra:

lim ƒ(x) / g(x)
x→a

= lim ƒ'(x) / g'(x)
   x→a

    Başka bir deyişle, L'Hôpital kuralı, uygun türdeki belirsiz biçimler ( 0/0 veya ∞/∞ ) için, sınırın her iki ifadenin ayırt edilmesiyle bulunabileceğini belirtir, bu da genellikle sınırı değiştirme yoluyla hesaplanabilen basitleştirilmiş bir ifadeyle sonuçlanır. L'Hôpital kuralının yalnızca bu özel durumlar için kullanılabileceğini ve tüm limitleri hesaplamak için kullanılamayacağını belirtmekte fayda var. Ayrıca, bazı durumlarda, limitin ikame yoluyla hesaplanabilmesi için L'Hôpital kuralının birden çok kez uygulanması gerekir; diğer durumlarda, L'Hôpital kuralı kaç kez uygulanırsa uygulansın, sonuç yine de belirsiz bir form olacaktır ve sınır mevcut olmayabilir veya farklı yöntemler kullanılarak değerlendirilmesi gerekebilir. Aşağıda L'Hôpital kuralının nasıl kullanılacağına dair bir örnek verilmiştir.

    Örnek

lim x - 1 / ln(x)
x→1

    Sınırın yerine 1 koymak, belirsiz 0/0 biçimiyle sonuçlanır:

lim x - 1 / ln(x) = 1 - 1 / ln(1) = 0/0
x→1

    Yukarıdaki ifade gerekli kriterlere uyduğundan, sınırı belirlemek için L'Hôpital kuralını kullanabiliriz:

lim x - 1 / ln(x)
x→1

= lim (x - 1)' / ln(x)'
   x→1

= lim 1/ 1/(x) = 1
   x→1

    Yukarıda bahsedildiği gibi, bazı durumlarda bir sınır belirleyebilmemiz için L'Hôpital kuralını birkaç kez uygulamamız gerekir. Aşağıda böyle bir örnek var.

    Örnek

lim x² / e^x
x→∞

    X ∞ yaklaştıkça, hem pay hem de payda sonsuza yaklaşır ve ∞/∞ belirsiz biçimiyle sonuçlanır. Böylece, L'Hôpital kuralını kullanabilir ve ifadeyi ayırt edebiliriz:

lim (x²)' / (e^x)'
x→∞

= lim 2x / e^x
   x→∞

    Sonuçta elde edilen ifadenin belirsiz ∞/∞ biçimine sahip olduğuna dikkat edin, bu nedenle sınırı hala belirleyemiyoruz ve bunun yerine ifadeyi bir kez daha ayırt ediyoruz:

lim (2x)' / (e^x)'
x→∞

= lim 2 / e^x
   x→∞

    İfadeyi ikinci kez farklılaştırdıktan sonra, artık belirsiz bir form olmayan bir ifade elde ederiz, böylece sınırı hesaplayabilir ve şunu bulabiliriz:

lim 2 / e^x = 0
x→∞

Diğer belirsiz formlar

    L'Hôpital kuralı sadece 0/0 ve ∞/∞ belirsiz formlarının sınırlarına uygulanabilse de, bazen ifadeleri L'Hôpital kuralını kullanmak için gerekli kriterleri karşılayacak şekilde cebirsel olarak yeniden düzenlemek mümkündür. Aşağıdaki örnekler bunu farklı durumlar için göstermektedir.

Belirsiz form: 0 · ∞

    Belirsiz formun sınırları 0 · ±∞, ürünü bölüm olarak yeniden yazarak belirsiz 0/0 veya ∞/∞ biçimine dönüştürülebilir; ve

lim g(x) = ±∞
x→a

verildiğinde

lim ƒ(x) = 0
x→a

f(x)'i yeniden yazabiliriz · bölüm olarak g(x),

ƒ / 1/g
veya
g / 1/ƒ

bu da belirsiz 0/0 veya ∞/∞ biçiminde bir ifadeyle sonuçlanır ve L'Hôpital kuralını uygulamamıza izin verir.

    Örnek

lim tan(x)(π/2 - x)
x→π/2

    π/2'nin takılması, belirsiz biçimde bir ifadeyle sonuçlanır 0 · ∞. L'Hôpital kuralından yararlanmak için, limiti, ikame 0/0 belirsiz biçiminde bir ifadeyle sonuçlanacak şekilde bir bölüm olarak yeniden yazın:

lim tan(x)(π/2 - x)
x→π/2

= lim π/2 - x / 1/tan(x)
   x→π/2

= lim π/2 - x / 1/cot(x)
   x→π/2

    Ardından, L'Hôpital kuralını kullanırız ve sınırı bulmak için ifadeyi farklılaştırırız:

lim (π/2 - x)' / cot(x)'
x→π/2

= lim -1 / csc²(x)
   x→π/2

= lim sin²(x) = 1
   x→π/2

Belirsiz formlar: 1^∞, 0⁰, ∞⁰

    1^∞, 0⁰, veya ∞⁰ belirsiz biçimlerinin sınırları, doğal logaritma fonksiyonu kullanılarak belirsiz 0/0 veya ∞/∞ biçiminin bir ifadesine dönüştürülebilir.

    Örnek

= lim sin(x)^tan(x)
   x→π/2

    π/2'yi sınıra takmak, belirsiz 1^∞ biçiminde bir ifade verir, bu nedenle ifadeyi L'Hôpital kuralını kullanmamıza izin veren bir forma sokmak için doğal logaritmayı sınıra uygularız:

ln(lim (sin(x)^tan(x)))
    x→π/2

= lim ln(sin(x)^tan(x))
   x→π/2

= lim tan(x)ln(sin(x))
   x→π/2

= lim sin(x)/cos(x) ln(sin(x))
   x→π/2

    sin(π/2) = 1 olduğundan, sin(x) terimini düşürebiliriz:

lim sin(x)/cos(x) ln(sin(x))
x→π/2

= lim ln(sin(x)) / cos(x)
   x→π/2

    sin(x) terimini bıraktıktan sonra, ifade artık 0/0 biçimindedir, bu nedenle L'Hôpital kuralını uygulayabiliriz:

lim (ln(sin(x)))' / cos(x)'
x→π/2

= lim cos(x)/sin(x) / -sin(x)
   x→π/2

= lim 0 / -1² = 0
   x→π/2

    Orijinal limitin doğal logaritmasını aldığımızı unutmayın, bu nedenle orijinal limiti bulmak için sonucumuzun üstünü almamız gerekir. Böylece, e⁰ = 1 ve sınır 1'dir.

    0⁰, ve ∞⁰ biçimindeki sınırlar bu örneğe benzer şekilde hesaplanabilir.

Belirsiz form: ∞ - ∞

    Belirsiz formun limitleri ∞ - ∞, limitin üs alınarak ve logaritma kuralları kullanılarak 0/0 veya ∞/∞ formunun limitine dönüştürülebilir. ƒ ve g'nin kesir olduğu durumlarda

lim ƒ(x) - g(x) = ∞ - ∞
x→a

, en küçük ortak paydayı kullanarak bunları tek bir bölümde birleştirebiliriz, ardından L'Hôpital kuralını kullanabiliriz.

    Örnekler

    Aşağıdaki sınırları bulun:

1.   lim (2/ln(x) - 2/ x - 1)
     x→1⁺




2.   lim (x - ln(x))
     x→∞

    1. x → 1⁺ olarak, ifade yaklaşımındaki her iki terim de ∞, bu nedenle sınır ∞ - ∞ biçimindedir. Her iki terim de kesir olduğundan, terimleri birleştirebiliriz,

lim (2/ln(x) - 2/ x - 1)
x→1⁺

= lim (2(x) - 2 - 2ln(x) / (x - 1)ln(x))
   x→1⁺

    L'Hôpital kuralını uygulamamıza izin veren 0/0 biçiminde bir ifadeyle sonuçlanır:

lim ((2(x) - 2 - 2ln(x))' / ((x - 1)ln(x))')
x→1⁺

= lim (2 - 2/x / ln(x) + (x - 1)1/x)
   x→1⁺

= lim (2x - 2 / xln(x) + (x - 1))
   x→1⁺

    Bu ifade yine belirsiz 0/0 biçimindedir, bu nedenle L'Hôpital kuralını bir kez daha uyguluyoruz:

lim (2x - 2 / xln(x) + (x - 1))
x→1⁺

= lim (2 / ln(x) + (1/x)x + 1)
   x→1⁺

= lim (2 / ln(x) + 2)
   x→1⁺

= lim 2 / 0+2 = 1)
   x→1⁺

    Bu nedenle, sınır 1'dir.

    2. x → ∞ olarak, her iki terim de ∞ yaklaşır, bu nedenle sınır ∞ - ∞ biçimindedir. Bu durumda, ifadenin terimleri kesir olmadığı için öncekiyle aynı yöntemi kullanamayız. Bunun yerine, denklemin her iki tarafını da üs alırız ve bazı gerçek sayıların L olduğunu varsayarsak:

L= lim (x - ln(x))
     x→∞

e^L= e^{lim_x→∞ (x - ln(x))}

e^L= lim e^{x - ln(x)}
       x→∞

e^L= lim e^x/e^ln(x)
       x→∞

e^L= lim e^x/x
       x→∞

    Ortaya çıkan ifade belirsiz ∞/∞ biçimindedir, bu nedenle L'Hôpital kuralını uygulayabiliriz:

e^L= lim (e^x)'/x'
       x→∞

e^L= lim e^x/1
       x→∞

e^L= ∞

    Böylece, sonsuz bir limit olan L = ∞, yani limitin mevcut olmadığını söyleyebiliriz.

L'Hôpital kuralı ne zaman kullanılmamalı?

    L'Hôpital kuralının herhangi bir limit için kullanılamayacağına dikkat etmek önemlidir. Tekrarlamak gerekirse, yalnızca limiti ikame yoluyla değerlendirdikten sonra 0/0 veya ∞/∞ belirsiz formlarıyla sonuçlanan ( veya dönüştürülebilen ) limitler için kullanılabilir. Durumun böyle olmadığı durumlarda kullanılması yanlış bir sonuca neden olacaktır.

    Örnek

lim 1 + cos(x) / e^x
x→0

    Bu sınır, ikame yoluyla değerlendirilebilir. x = 0'ı limite takmak,

lim 1 + cos(x) / e^x = 1+1 / 1 = 2
x→0

    Sınırın 2 olduğunu görüyoruz. Ancak, yukarıda yaptığımız gibi limiti hesaplamak yerine L'Hôpital kuralını uygulamış olsaydık, yanlış bir limit bulurduk:

lim (1 + cos(x))' / (e^x)'
x→0

= lim -sin(x) / e^x
   x→0

= 0/1 = 0

    Bu nedenle, L'Hôpital kuralını bir sınıra uygulamadan önce ikame kullanarak uygun formun bir sınırına sahip olduğumuzu doğrulamak önemlidir.

    Ayrıca, bir sınırın belirsiz biçimde 0/0 veya ∞/∞ olduğu durumlarda bile, bunun sınırın var olduğunu veya L'Hôpital kuralı kullanılarak belirlenebileceğini garanti etmediğini belirtmek de önemlidir. L'Hôpital kuralının tekrarlanan uygulamalarının her zaman belirsiz bir biçimde sonuçlanması tamamen mümkündür. Bu gibi durumlarda, sınır mevcut olmayabilir. Bununla birlikte, L'Hôpital kuralı kullanılarak bir sınırın belirlenememesi, sınırın var olmadığı anlamına gelmez; Bazen, limiti hesaplamak için başka yöntemler kullanmak mümkün olabilir.

    Örnek

lim x + 1 / √ x² + 2x + 3
x→∞

    x → ∞ olarak, her iki terim de ∞ yaklaşır, bu nedenle ∞/∞ belirsiz formunun bir sınırına sahibiz ve L'Hôpital kuralını uygulayabiliriz:

lim (x + 1)' / (√ x² + 2x + 3)'
x→∞

= lim 1/ (x + 1)/(√ x² + 2x + 3)
   x→∞

= lim √ x² + 2x + 3 / x + 1
   x→∞

    Ortaya çıkan sınır hala ∞/∞ biçimindedir ve L'Hôpital'in kuralını bir kez daha uygularsak, başladığımız sınırla aynı sonuca ulaşırız. L'Hôpital kuralını kaç kez uygularsak uygulayalım, aynı iki sonuç arasında gidip gelmeye devam edeceğiz. Bu nedenle, bu sınır L'Hôpital kuralı kullanılarak hesaplanamaz. Bununla birlikte, ifadeyi cebirsel olarak basitleştirerek hesaplanabilir. Bunu yapmak için önce x + 1'i

√(x + 1)²

olarak yeniden yazıyoruz. Ayrıca x² + 2x + 3 = (x + 1)² + 2 olduğunu bulmak için paydanın karesini tamamlıyoruz, bu da ifadeyi basitleştirmemize izin veriyor:

lim x + 1 / √ x² + 2x + 3
x→∞

= lim √(x + 1)² / √ (x + 1)² + 2
   x→∞

= lim √ 1/  (x + 1)² + 2 / (x + 1)²
   x→∞

= lim √ 1/  1+  2/(x + 1)²
   x→∞

= √ 1/  1 + 0

= 1