Türev Nedir, Ne İşe Yarar?
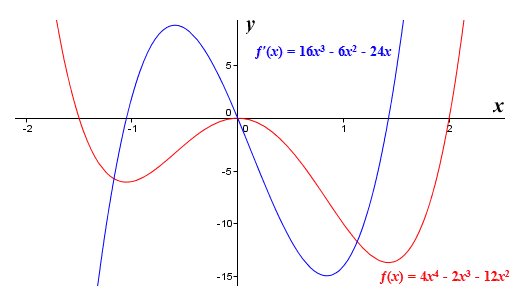
Türevler, bir fonksiyonun bağımsız bir değişkene göre değişen değişim oranı olarak tanımlanır. Türev öncelikle değişen bir miktar olduğunda kullanılır ve değişim oranı sabit değildir. Türev, bir değişkenin ( bağımlı değişken ) başka bir değişkene ( bağımsız değişken ) göre duyarlılığını ölçmek için kullanılır. Bu yazımızda türevlerin ne olduğunu, türevlerin tanımını, Math'ı, limitlerini ve türevlerini detaylı olarak ele alacağız.
ƒ'(x) = Δy / Δx
= lim ƒ(x + h) - ƒ(x) / h
h→0
Türev Anlamları
Matematikte türevler, bir miktarın diğerine göre anlık değişim oranını ifade eder. Bir miktarın an be an doğasını araştırmaya yardımcı olur.
Türev Örnek:
Bir arabanın 'a' noktasından 'b' noktasına hareket etmesinin 't' saniye sürmesine izin verin.
Fakat 'a' noktasından 'c' noktasına geçmek ne kadar sürer?
Veya
'T-1' saniyelerinde ne kadar mesafe kat edecek?
Bu, aşağıdaki gibi hızdan bilinebilir:
Hız (v) = d(x)/d(t)
Burada 'x' kat edilen mesafedir ve 't' bu mesafeyi kat etmek için geçen süredir.
Bu size birim zaman başına kat edilen mesafeyi verecektir, böylece herhangi bir zaman aralığında kapsanan herhangi bir mesafeyi analiz edebiliriz.
Matematikte Türevler – Kalkülüs
Türevi bulma sürecine farklılaşma denir. Ters sürece anti-farklılaşma denir. y = f(x) fonksiyonunun türevini bulalım. Y değerinin, x değişkeninin değişimine göre değiştiği oranın ölçüsüdür. X değişkenine göre "f" fonksiyonunun türevi olarak bilinir.
Eğer x'teki sonsuz küçük bir değişiklik dx olarak gösterilirse, y'nin x'e göre türevi dy/dx olarak yazılır.
Burada x'e göre y'nin türevi "dy by dx" veya "dy over dx" olarak okunur.
Örnek:
'Y' bağımlı bir değişken ve 'x' bağımsız bir değişken olsun.
x'in değerindeki bir değişikliği düşünün, yani dx.
X'teki bu değişim, y'de bir değişiklik getirecektir, bırakın bu ölsün.
Şimdi x'teki birim değişimi ile y'deki değişimi aşağıdaki gibi bulmak için:
f(x), x'in değeri değiştikçe değeri de değişen bir fonksiyon olsun
Türevi bulma adımları:
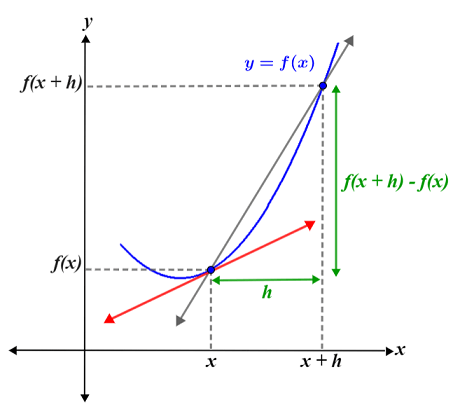
- X'i mümkün olan en küçük değerle değiştirin ve bunun 'h' olmasına izin verin ve böylece işlev f (x + h) olur.
- İşlev değerindeki değişikliği elde edin: f(x + h) – f(x)
- 'x'ten 'x+h'ye geçerken f(x) fonksiyonundaki değişim oranı şöyle olacaktır:
Δy / Δx
= lim ƒ(x + h) - ƒ(x) / h
h→0
Şimdi d(x) göz ardı edilebilir çünkü çok küçük olduğu düşünülür.
Türev Formülleri
Doğrusal, üstel ve logaritmik fonksiyonlar gibi bazı fonksiyonlar için türev formülleri aşağıda listelenmiştir:
- d/dx (k) = 0, burada k herhangi bir sabittir
- d/dx(x) = 1
- d/dx(xn) = nxn-1
- d/dx (kx) = k, burada k herhangi bir sabittir
- d/dx (√x) = 1/2√x
- d/dx (1/x) = -1/x2
- d/dx (log x) = 1/x, x > 0
- d/dx (ex) = ex
- d/dx (ax) = ax log a
Türev Çeşitleri
Türevler, birinci ve ikinci dereceden türevler gibi sıralarına göre farklı tiplerde sınıflandırılabilir. Bunlar aşağıda verildiği gibi tanımlanabilir.
Birinci Dereceden Türev
Birinci dereceden türevler, fonksiyonun yönünü fonksiyonun arttığını veya azaldığını söyler. İlk türev matematiği veya birinci dereceden türev, anlık bir değişim oranı olarak yorumlanabilir. Teğet çizgisinin eğiminden de tahmin edilebilir.
İkinci Dereceden Türev
İkinci dereceden türevler, verilen fonksiyon için grafiğin şekli hakkında bir fikir edinmek için kullanılır. Fonksiyonlar konkavite açısından sınıflandırılabilir. Verilen grafik fonksiyonunun konkavitesi iki tipte sınıflandırılır:
- İçbükey Yukarı
- İçbükey Aşağı
Kalkülüs - Türev Örneği
f(x), f(x) = x2 olan bir fonksiyon olsun
x2'in türevi 2x'tir, yani x'teki her birim değişiminde, fonksiyonun değeri iki katına (2x) dönüşür.
Limitler ve Türevler
Dx o kadar küçük yapıldığında bu neredeyse hiçbir şey haline gelmiyor. Limitler ile, x'in sıfıra yaklaştığını ancak sıfır olmadığını söylemek istiyoruz.
Matematiksel olarak: tüm gerçek ε > 0 için gerçek bir δ > 0 vardır, öyle ki 0 < |x − c| < δ, ( burada c ∈ R ) |f(x) − L| < ε
Temel Kavramlar
- Paydada bulunan x'in bir gücünü ayırt etmek için, önce onu negatif üslü bir güç olarak ifade edin. Örneğin.
1/x2=x−2
- Türev kuralları, polinom fonksiyonlarını ayırt etme sürecini basitleştirir.
- Bir radikali ayırt etmek için, önce, onu rasyonel bir üsse sahip bir güç olarak ifade edin
Anlık değişim oranı problemini çözmek için türev kuralları uygulayın
Bir skydiver 2200 m yükseklikten bir uçaktan atlar. Skydiver'ın yerden yüksekliği, metre cinsinden, t saniye sonra h(t) = 2200 – 4.9t2 fonksiyonu ile temsil edilir ( hava direncinin bir faktör olmadığını varsayarsak ). Skydiver 4 saniye sonra ne kadar hızlı düşüyor?
Çözüm
Skydiver'ın yüksekliğinin herhangi bir zamanda anlık değişim hızı, yükseklik fonksiyonunun türevi ile temsil edilir.
y(t) = 2200 – 4.9t2
h'(t) = 0 – 4,9 (2t) = -9,8 t
4 s'deki anlık değişim oranını bulmak için t = 4'ü türev fonksiyonuna yerleştirin.
h'(t) = – 9.8 (4) = -39.2
4 sn sonra, skydiver 39.2 m/s oranında düşüyor.
Trigonometrik Fonksiyonların Türevleri
Ayrıca günah, cos, tan ve benzeri anlamlara gelen trigonometrik fonksiyonların türevini de bulabiliriz . Formüller aşağıda verilmiştir:
- d/dx (sin x) = cos x
- d/dx (cos x) = -sin x
- d/dx (tan x) = sec2x
- d/dx (cosec x) = -cosec x cot x
- d/dx (sec x) = sec x tan x
- d/dx (cot x) = -cosec2x
Tan x türevi
Tan x'in türevi, aşağıda gösterildiği gibi bölüm kuralı kullanılarak türetilebilir:
f(x) = tan x olsun
Biliyoruz ki tan x = sin x / cos x
u = sin x ve v = cos x alalım
Bildiğimiz gibi,
d/dx (u/v) = [v(du/dx) – u(dv/dx)]/ v2
d/dx (sin x/cos x) = [cos x(d/dx)sin x – sin x(d/dx)cos x]/ cos2x
= [cos x . cos x – sin x . (-sin x)] /cos2x
= (cos2x + sin2x)/cos2x
Kimlik sin kullanma sin2A + cos2A = 1,
= 1/cos2x
= sec2x [1/cos x = sec x olduğundan]
d/dx (tan x) = sec2x
Bu nedenle, tan x'in türevi sec2x.
1/x türevi
1/x türevi aşağıda verildiği gibi türetilebilir:
d/dx (1/x) = d/dx (x-1)
Biliyoruz ki d/dx (xn) = nxn-1
Burada, n = -1
d/dx(1/x) = d/dx (x-1) = (-1)x(-1 – 1)
= -x-2
= -1/x2
Bu nedenle, 1/x'in türevi -1/x2.
Türevlerin Özellikleri
Türevler daha küçük parçalara ayrılabilir, böylece verilen ifadeler kolayca değerlendirilebilir. İfadeleri veya işlevleri bölme sürecinde, terimler artı ( + ), eksi ( - ) veya bölme ( / ) gibi işleçlere göre ayrılır. Bu, aşağıda verilen örnekler kullanılarak daha iyi anlaşılabilir.
Türev Örnekleri
Örnek 1: f(x) = 5x2 – 2x + 6 fonksiyonunun türevini bulun.
Çözüm:
Verilen
f(x) = 5x2 – 2x + 6
Şimdi f(x)'in türevini alarak,
d/dx f(x) = d/dx (5x2 – 2x + 6)
Fonksiyonun terimlerini şu şekilde ayıralım:
d/dx f(x) = d/dx (5x2) – d/dx (2x) + d/dx (6)
Formülleri kullanarak:
d/dx (kx) = k ve d/dx (xn) = nxn-1
⇒ d/dx f(x) = 5(2x) – 2(1) + 0 = 10x – 2
Örnek 2: 2 tan x + 1 türevini bulun
Çözüm:
Verilen fonksiyon f(x) = 2 tan x + 1 olsun
Şimdi, türevi alarak,
d/dx f(x) = d/dx (2 tan x + 1)
= d/dx (2 tan x) + d/dx (1)
= 2 (sec2x) + 0
= 2 sec2x
Sıkça Sorulan Sorular – SSS
S1. Matematikte türev nedir?
Matematikte türev, eş zamanlı değişim oranını gösteren yöntem olarak tanımlanır. Bu, verilen işlevin belirli bir noktada değiştiği miktarı temsil etmek için kullanıldığı anlamına gelir.
S2. Finansta türevler nelerdir?
Finansta, bir türev, değeri üzerinde anlaşmaya varılmış bir dayanak finansal varlığa veya sırasıyla menkul kıymet ve endeks gibi varlık kümesine dayanan iki veya daha fazla taraf arasındaki bir sözleşmedir.
S3. Türev formülü nedir?
y = f(x) fonksiyonunun türevi dy/dx = d/dx f(x) olarak ifade edilebilir, burada dy/dx, x'e göre y'nin türevi olarak adlandırılır ve d/dx f(x), x'e göre f(x)'in türevidir.
S4.Türev sembolü nedir?
Bir f(x) fonksiyonunun türevini belirtmek için kullanılan sembol d/dx f(x) veya f'(x) şeklindedir. Eğer fonksiyon y kullanılarak temsil ediliyorsa, birinci dereceden ve ikinci dereceden türevleri sırasıyla y' ve y'' olarak gösterilir.
S5. Neden türev olarak adlandırılıyor?
Türev teriminin, başka bir şey olduğu gerçeğinden, yani orijinal f(x) fonksiyonu tarafından belirtilen farklı f′(x) fonksiyonundan türetildiği varsayılmaktadır. Böylece, f'(x) diğer fonksiyondan türetilmiştir, diyelim ki f(x).
Türev Nerelerde Kullanılır?
Türevin kullanım alanları oldukça geniştir ve pek çok bilim ve mühendislik dalında temel bir rol oynar. İşte bazı örnekler:
- Fizik: Fizikte hareket analizi, kinematik ve dinamik problemler genellikle türev hesaplamaları kullanılarak çözülür. Hız, ivme ve kuvvet gibi fiziksel büyüklüklerin değişimini anlamak için türevlerden yararlanılır.
- Mühendislik: Türevler, elektrik, mekanik, kimya ve diğer mühendislik disiplinlerinde yaygın bir şekilde kullanılır. Elektrik devrelerinin analizi, malzeme mühendisliği, ısı transferi gibi konularda türevlerin kullanımı yaygındır.
- Ekonomi: Ekonomi ve finans alanında, türevlerin kullanımı oldukça önemlidir. Fiyat değişimlerinin analizi, yatırım stratejilerinin belirlenmesi ve risk yönetimi gibi konularda türev hesaplamalarına başvurulur.
- İstatistik: İstatistiksel analizlerde türevler, olasılık dağılımlarının özelliklerini anlamak için kullanılır. Örneğin, bir olasılık yoğunluk fonksiyonunun en büyük değeri olan maksimum noktasını bulmak için türevlerden yararlanılır.
- Bilgisayar Bilimi: Bilgisayar grafikleri, yapay zeka ve veri analizi gibi alanlarda türevler önemli bir rol oynar. Özellikle makine öğrenmesi ve derin öğrenme algoritmalarında gradyan hesaplamaları ( bir fonksiyonun türevinin hesaplanması ), model eğitimi ve optimizasyonunda kullanılır.
Bu sadece bazı örneklerdir ve türevin kullanım alanları oldukça geniştir. Türev hesaplamaları, bir fonksiyonun anlık değişimini ve orantılı olduğu kavramları anlamamızı sağlar. Bu nedenle matematiksel analiz, bilimsel araştırmalar ve teknolojik gelişmeler için vazgeçilmez bir araçtır.