Elektrostatik nedir?

BİLİM ve TEKNOLOJİ 25.05.2023 514 0

Elektrostatik, adından da anlaşılacağı gibi, durağan elektrik yüklerinin incelenmesidir. Kürk ile ovulan bir plastik çubuk veya ipek ile ovulan bir cam çubuk, küçük kağıt parçalarını çeker ve elektrik yüklü olduğu söylenir. Kürk ile ovulan plastik üzerindeki yük negatif , ipek ile ovulan cam üzerindeki yük ise pozitif olarak tanımlanır .

Elektrik şarjı

Elektrik yüklü nesnelerin birkaç önemli özelliği vardır:

Benzer yükler birbirini iter; yani pozitif pozitifi iter ve negatif negatifi iter.

Farklı yükler birbirini çeker; yani pozitif negatifi çeker.

Şarj korunur. Nötr bir nesnenin net yükü yoktur. Plastik çubuk ve kürk başlangıçta nötr ise, çubuk kürk tarafından yüklendiğinde, kürkten çubuğa negatif bir yük aktarılır. Çubuktaki net negatif yük, kürkteki net pozitif yüke eşittir.

İletken , elektrik yüklerinin kolayca akabileceği bir malzemedir. Bir yalıtkan , elektrik yüklerinin kolayca hareket etmediği bir malzemedir. Bir elektroskop , yükün varlığını göstermek için kullanılan basit bir cihazdır. Şekil 1'de gösterildiği gibi, elektroskop, bir iletken topuzdan ve eklenmiş hafif iletken yapraklardan oluşur - genellikle altın varak veya alüminyum folyodan yapılır. Yüklü bir nesne topuza dokunduğunda, benzer yükler iter ve yaprakları birbirinden ayırmaya zorlar. Elektroskop, yükün varlığını gösterecektir, ancak yükün pozitif mi yoksa negatif mi olduğunu doğrudan göstermez.

Şekil 1

Bir elektroskop yükün varlığını bildirir.

Nötr bir elektroskobun yakınındaki büyük bir yük, yaprakların birbirinden uzaklaşmasına neden olabilir. Elektroskop iletken malzemeden yapılmıştır, bu nedenle pozitif yükler, yakındaki ( ancak dokunmayan ) negatif yüklü çubuk tarafından topuza çekilir. Yapraklar negatif bir yük ile bırakılır ve bu nedenle sapar. Negatif çubuk çıkarıldığında yapraklar düşer.

Şimdi, yüklü çubuk yakındayken elektroskop düğmesine parmağınızla dokunmayı düşünün. Elektronlar itilecek ve elden elektroskoptan dışarı akacaktır. Yüklü çubuk hala yakındayken el çekilirse , elektroskop bir yük tutacaktır. Bu şarj yöntemine indüksiyonla şarj denir ( bkz. Şekil 2 ).

Şekil 2

İndüksiyonla bir elektroskobun şarj edilmesi.

Bir cisim yüklü bir çubukla sürtüldüğünde, cisim yükü paylaşır ve böylece her ikisinin de yükü aynı işarette olur. Buna karşılık, indüksiyonla şarj etme, bir nesneye yüklü çubuğun zıt yükü verir.

Yükler malzeme boyunca serbestçe dolaşamasa da, yalıtkanlar indüksiyonla yüklenebilir. Yakındaki büyük bir yük - dokunmadan - yalıtkanın yüzeyinde zıt bir yüke neden olur. Şekil 3'te gösterildiği gibi, moleküllerin negatif ve pozitif yükleri hafifçe yer değiştirmiştir. Yalıtkandaki yüklerin bu yeniden hizalanması etkili bir indüklenmiş yük üretir.

Şekil 3

Yakındaki bir yüklü nesne tarafından bir yalıtkan üzerinde yüzey yükünün indüksiyonu.

Coulomb yasası

Coulomb yasası, iki yük arasındaki elektrostatik kuvvetin ( F ) büyüklüğünü verir:

burada q 1 ve q 2 yüklerdir, r aralarındaki mesafedir ve k orantı sabitidir. Şarj için SI birimi coulomb'dur. Yük coulomb cinsinden ve mesafe metre cinsindense, k için aşağıdaki yaklaşık değer kuvveti newton cinsinden verecektir: k = 9,0 × 10⁹ N · m²/C². Elektrostatik kuvvetin yönü, yüklerin işaretlerine bağlıdır. Benzer yükler iter ve farklı yükler çeker.

Coulomb yasası , boş uzayın geçirgenliği olarak bilinen başka bir sabit ( ε₀ ) cinsinden de ifade edilebilir :

Geçirgenlik sabiti kullanıldığında, Coulomb yasası

En temel elektrik yükü, bir protonun veya bir elektronun yüküdür. Bu değer (e) , e = 1,602 × 10⁻¹⁹ coulomb'dur. Bir coulomb'un yüküne eşit olmak için yaklaşık 6.24 × 1018 fazla elektron gerekir ; bu nedenle, çok büyük bir statik yüktür.

Bir ücret sistemi için, her bir yük grubu arasındaki kuvvetler bulunmalıdır; o zaman, belirli bir yük üzerindeki net kuvvet, bu kuvvetlerin vektörel toplamıdır. Aşağıdaki problem bu prosedürü göstermektedir.

Örnek 1: Coulomb cinsinden değeri bilinmeyen Q'nun eşit yüklerini ele alalım . Bu yüklerden ikisi arasındaki X mesafesindeki kuvvet F'dir . Şekilde, B noktasından X uzaklığı olan A noktasına üç yük ( 3Q ) yerleştirilmiştir . Bir yük ( Q ) , tek yüke sahip C noktasından X / 2 uzaklıktaki B noktasına yerleştirilmiştir. B noktasında yüke etkiyen net kuvvet nedir ?

Şekil 4

Örnek için puan ücretlerinin düzenlenmesi.

Çözüm : Bu problem orantılı akıl yürütme yoluyla çözülebilir. B'deki bir yük üzerindeki 3 Q'nun kuvveti 3 F olacaktır . Tek yük B'den X'in yarısı olduğundan , kuvvet X mesafesinden dört kat daha büyük olacaktır , yani 4 F olacaktır . 3 F ve 4 F kuvvetleri dik açıdadır ve bu nedenle bileşke kuvvet 5 F veya

Yön teğetten bulunur: θ −1 = tan 4/3 = 53°

Elektrik alanları ve kuvvet çizgileri

Küçük bir pozitif test yükü, büyük bir pozitif yükün yanına getirildiğinde, büyük yükten uzağa yönlendirilen bir kuvvetle karşılaşır. Test yükü büyük yükten uzaktaysa, Coulomb yasası tarafından verilen elektrostatik kuvvet, yakın olduğu duruma göre daha küçüktür. Sabit bir yük veya sabit yükler kümesinden kaynaklanan bir elektrostatik kuvvetin yönü ve büyüklüğüne ilişkin bu veriler, bir elektrostatik alan oluşturur. Elektrik alan, o noktaya yerleştirilmiş küçük bir pozitif test yüküne ( q 0 ) uygulanan birim yük başına kuvvet olarak tanımlanır. Matematiksel olarak,

Hem kuvvetin hem de elektrik alanın vektörel büyüklükler olduğuna dikkat edin. Test yükünün alanı, incelenmekte olan sabit yüklerin alanını etkilemeyecek şekilde küçük olmalıdır. Elektrik alan için SI birimi, coulomb başına newton'dur ( N / C ).

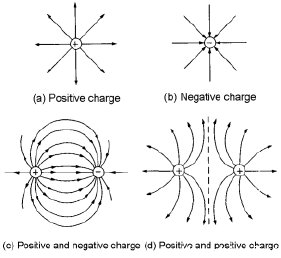
Şekil 5, bir pozitif yükü ve bir negatif yükü çevreleyen elektrik alanlarının resimsel bir temsilidir. Bu çizgilere alan çizgileri veya kuvvet çizgileri denir .

Şekil 5

(a) pozitif ve (b) negatif nokta yüklerin elektrik alan çizgileri.

Şekil 6, zıt yükler, benzer yükler ve zıt yüklü plakalar için elektrik alanlarını göstermektedir.

Şekil 6

(a) iki zıt yükün, (b) iki benzer yükün ve (c) zıt yüklü iki levhanın elektrik alan çizgileri.

Yüklerin herhangi bir statik konfigürasyonu için elektrik alan çizgileri çizme kuralları şunlardır:

Çizgiler pozitif yüklerle başlar ve negatif yüklerle biter.

Bir yükten çıkan veya üzerinde sonlanan çizilen çizgilerin sayısı, yükün büyüklüğü ile orantılıdır.

Ücretsiz bir bölgede hiçbir zaman iki alan çizgisi kesişmez. ( Alan çizgisine teğet bileşke kuvvetin yönünü temsil ettiğinden, her noktada yalnızca bir çizgi olabilir. )

Çizgi, iletken yüzeye dik olarak yaklaşır.

Elektrik akımı

Elektrik akısı, belirli bir yüzeyden geçen alan çizgilerinin sayısı olarak tanımlanır. Şekilde, bir noktasal yükten çıkan elektrik akısı çizgileri, yükün merkezinde olduğu hayali bir küresel yüzeyden geçmektedir.

Şekil 7

Bir nokta yükünden kaynaklanan elektrik akısı + q .

Bu tanım şu şekilde ifade edilebilir: Φ = ∑E · A, burada Φ ( Yunanca phi harfi ) elektrik akısıdır, E elektrik alanıdır ve A alan çizgilerine dik alandır. Elektrik akısı N · m²/C² cinsinden ölçülür ve skaler bir miktardır. Ele alınan yüzey alan çizgilerine dik değilse, ifade Φ = ∑ EA cos θ şeklindedir.

Genel anlamda akı, elektrik alan vektörü ile ΔA vektörünün iç çarpımının kapalı integralidir. ΔA'nın yönü, sanal yüzeye dik olarak dışa doğru çizilmiştir. Matematiksel olarak, Φ = ΦE · d A. Kabul edilen kural, akı çizgilerinin bir yüzeyden çıkarsa pozitif, bir yüzeye giriyorsa negatif olmasıdır.

Gauss yasası

Gauss yasası, herhangi bir elektrik alanını hesaplamak için bir yöntem sağlar; bununla birlikte, tek pratik kullanımı, sabit yüklerin oldukça simetrik dağılımlarının olduğu alanlar içindir. Yasa, herhangi bir gerçek veya hayali kapalı yüzeyden geçen net elektrik akısının, o yüzeyin içindeki net elektrik yükünün ε ile bölümüne eşit olduğunu belirtir. Sonuç olarak, belirli bir kapalı yüzeyde hiçbir yük yoksa, yüzeye giren ve çıkan akı çizgileri vardır. Gauss yasasını uygulamak için gerekli hayali yüzeye gauss yüzeyi denir . cebirsel olarak,

veya ayrılmaz biçimde,

burada θ, E yönü ile yüzeye normalin dışa doğru yönü arasındaki açıdır ve ε geçirgenlik sabitidir.

Bir nokta yükünden kaynaklanan elektrik alanın hesaplanmasını düşünün. Şekil, nokta yükünü, alanının yönünü ve bir gauss yüzeyini göstermektedir. Elektrik alan gauss yüzeyine dik olduğundan ve dışa doğru yönlendirildiğinden, θ 90 derecedir ve cos θ = 1'dir. Gauss yasası şu şekildedir:

Bir kürenin alanında değiştirin ve sol taraf şuna indirgenir:

veya

bu, Coulomb yasasından elde edilen ifadenin aynısıdır ve elektrik alanın kuvvet cinsinden tanımıdır.

İnce iletken bir yük kabuğu nedeniyle alan ifadesinin türetilmesi aşağıdadır. Şekil 8, (a) yarıçaplı ( R ) bir kabuk için elektrik alanları, (b) kabuğun dışı için gauss yüzeyini ve (c) yarıçaplı ( r ) için (c) kabuğun içi için gauss yüzeyini göstermektedir.

Şekil 8

R yarıçaplı yüklü küresel bir kabuk . (b) yarıçapı r > R olan bir gauss küresi . (c) yarıçapı r < R olan bir gauss küresi .

Yük kabuğunun dışındayken, Şekil (a)'daki gibi, Gauss denkleminin sol tarafı, bir nokta yük için verilen aynı nedenlerle aşağıdaki ifadeye indirgenir:

Öyleyse,

Böylece, bir yük küresinin dışındaki elektrik alan, kürenin merkezinde bulunan bir noktada aynı miktarda yük toplanmış gibi aynıdır.

Kürenin içindeki gauss yüzeyi hiçbir yük içermez ve bu nedenle, düzgün yüklü küresel kabuğun içinde elektrik alanı yoktur. Aynı ispat katı bir iletken için de geçerlidir, çünkü iletkenin tüm yükü yüzeyde bulunur. Düzensiz şekilli bir iletkenin içindeki elektrik alan bile sıfır olduğundan, yük düzensiz bir şekle eşit olarak dağılmayacaktır. Şarj, iletkenin dışındaki çıkıntılı noktalarda birikme eğiliminde olacaktır.

Potansiyel fark ve eşpotansiyel yüzeyler

Önceki örneklerde yük dağılımları küreseldi ve bu nedenle gauss yüzeyi bir küreydi. Bir yük tabakasının veya bir yük hattının elektrik alanını bulurken, kullanılacak doğru gauss yüzeyi bir silindirdir.

Örnek 2: İletken olmayan sonsuz bir yük tabakasının elektrik alanını bulun. Elektrik alanı, her iki taraftaki levhadan dışarıya doğru yönlendirilir. Birim alan başına ücret σ'dır ( Yunanca sigma harfi ). Elektrik alanı ve gauss yüzeyi için Şekil'e bakın.

Şekil 9

Bir gauss silindiri, sonsuz bir yük tabakasının üstünde ve altında uzanmalıdır.

Kapalı silindirik gauss yüzeyinin alanı, sol uç, sağ uç ve duvarın alanlarının toplamı olacaktır; bu nedenle, ∑ EA cos θ = ( EA cos θ ) sol uç + ( EA cos θ ) sağ uç + ( EA cos θ ) duvar . Elektrik alan, duvar alanının dış normaline dik açılarda olan duvara paraleldir; bu nedenle sağdaki son terim sıfırdır. Her bir uçta, E dış normal ile aynı yöndedir, yani ( EA cos θ ) sol uç + ( EA cos θ ) sağ uç = 2 EA , burada A gauss silindirinin ucunun alanıdır. Gauss yüzeyi içindeki toplam yük, birim alan ve alan başına yükün çarpımıdır; Bu yüzden

Elektrik alanın büyüklüğünün plakadan olan uzaklığa bağlı olmadığına dikkat edin. Elektrik alan üniformdur. Sonlu yük plakalarının pratik durumunda, elektrik alan, yüklü plakaya nispeten yakındır.

İki paralel levhanın bileşke elektrik alanı, aynı yüke sahip bir levhanınkinin iki katıdır:

veya

burada q , her bir plaka üzerindeki yük ve A, her bir plakanın alanıdır. Plakalar zıt yüklere sahipse, elektrik alan plakalar arasında var olacak ve plakaların dışında sıfır olacaktır. Yükler eşit işaretliyse, elektrik alan plakalar arasında sıfır olacaktır ve plakaların dışında yukarıdaki denklem ile ifade edilecektir. Bu sonuçlar Gauss yasası ile elde edilebilir.

Elektrostatik potansiyel ve eş potansiyel yüzeyler

Paralel plakalar arasındaki düzgün alan içinde A noktasından B noktasına küçük bir test yükü q ' hareket ettirdiğinizi hayal edin. Yükü aktarırken yapılan iş, mekanik bölümünde verilen aynı iş tanımını kullanarak, test yükü üzerindeki kuvvet ile yer değiştirmenin paralel bileşeninin çarpımına eşittir. Bu çalışma , elektrik alanın tanımından kuvvetin yüke oranı olarak da E cinsinden ifade edilebilir : W · d, E = F/ q ve W = q ′. Şekil 10'a bakın.

Şekil 10

Bir E elektrik alanında q' A konumundan B konumuna hareket ettiğinde iş yapılır.

İş, potansiyel enerjideki değişimdir: U B − U A = q ′ Ed .

Genel olarak, bazen elektrik potansiyeli farkı olarak adlandırılan elektrostatik potansiyel farkı , birim pozitif yük başına enerji değişimi veya V B − V A = ( U B − U A ) / q ′ olarak tanımlanır. Belirli elektrik alan konfigürasyonları için, elektrostatik potansiyelin integral tanımını kullanmak gerekli olabilir:

burada bir test yükü, bir elektrik alanında ( E ) s yolu boyunca A noktasından B noktasına bir çizgi integrali üzerinde hareket eder .

Paralel plakaların özel durumu için:

burada V, volt ( V ) birimiyle ölçülen plakalar arasındaki potansiyel farktır:

Noktasal yükten ( r ) uzaktaki bir noktasal yükten ( q ) kaynaklanan elektrik potansiyeli,

Aşağıdaki problem, noktasal yüklerden kaynaklanan elektrik alan ve potansiyel hesaplamalarını göstermektedir.

Örnek 3: Aralarında X mesafesi olan +3 Q ve – Q yüklü iki yük verildiğinde , aşağıdakini bulun: (1) Doğru boyunca hangi nokta(lar)da elektrik alan sıfırdır? (2) Hangi nokta(lar)da elektrik potansiyeli sıfırdır? ( Bkz. Şekil 11 )