Ömer Hayyam Kimdir? Ömer Hayyam'ın Hayatı, Eserleri (Kitapları)

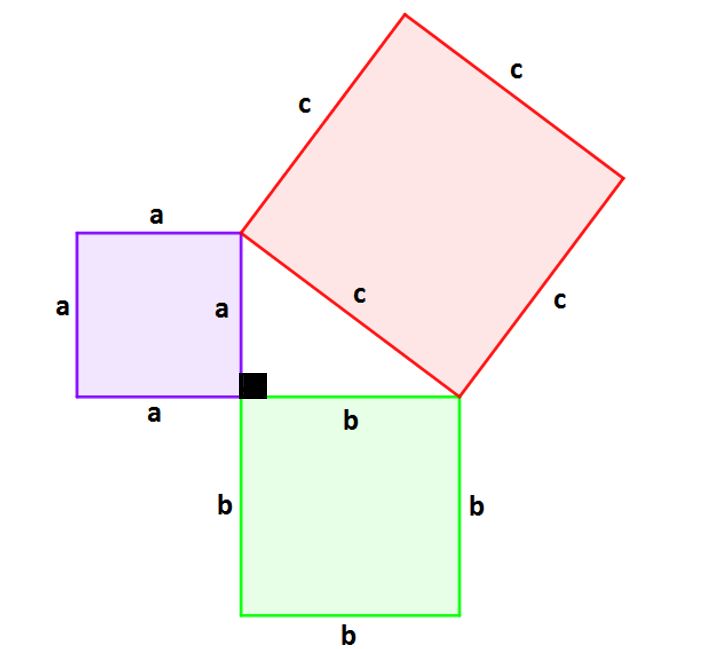
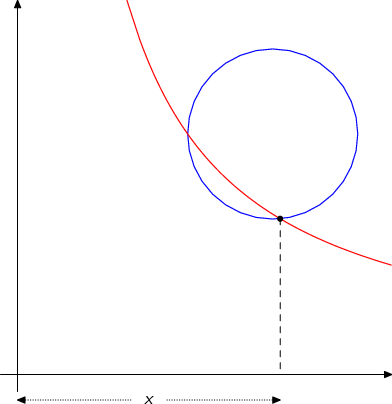
    Ömer Hayyam , matematikçi olduğu kadar şair de olan bir İslam alimiydi. Astronomik tablolar derledi ve takvim reformuna katkıda bulundu ve bir parabol ile bir daireyi keserek kübik denklemleri çözmenin geometrik bir yöntemini keşfetti.

Doğumu

18 Mayıs 1048 
Nişabur, İran ( şimdiki İran )

Ölümü

4 Aralık 1131 
Nişabur, İran ( şimdiki İran )

Ömer Hayyam Kimdir? Hayatı, Eserleri, Edebi Kişiliği

    Ömar Khayyam'ın tam adı Ghiyath al-Din Abu'l-Fath Umar ibn Ibrahim Al-Nisaburi al-Khayyami'dir. El-Hayyami ( veya el-Hayyam ) adının gerçek çevirisi 'çadır yapımcısı' anlamına gelir ve bu, babası İbrahim'in mesleği olabilir. Hayyam, yazdığı zaman kendi adının anlamı üzerinde oynadı:

    11. yüzyılın siyasi olayları Hayyam'ın hayatında büyük rol oynamıştır. Selçuklu Türkleri, 11. yüzyılda güneybatı Asya'yı işgal eden ve sonunda Mezopotamya, Suriye, Filistin ve İran'ın çoğunu içine alan bir imparatorluk kuran kabilelerdi . Selçuklular, Horasan'ın otlaklarını işgal etti ve daha sonra 1038 ile 1040 arasında , kuzeydoğu İran'ın tamamını fethettiler. Selçuklu hükümdarı Tuğrul Bey, 1038'de Nişabur'da kendini padişah ilan etti ve 1055'te Bağdat'a girdi.. Hayyam, ortodoks bir Müslüman devlet kurmaya çalışırken dini sorunları da olan bu zor, istikrarsız askeri imparatorlukta büyüdü.

    Hayyam Naishapur'da felsefe okudu ve arkadaşlarından biri şöyle yazdı: 

... zeka keskinliği ve en yüksek doğal güçlerle donatılmış ...

    Bununla birlikte, bu, bilginlerin, hatta Hayyam gibi bilginlerin bile, birçok saraydan birinde bir hükümdarın desteğini almadıkça hayatı kolay bulduğu bir imparatorluk değildi. Yerel siyaset ve yerel askeri rejimin kaderi, herhangi bir zamanda kimin iktidarda olduğunu belirlediğinden, böyle bir himaye bile çok fazla istikrar sağlamayacaktır. Hayyam, Cebir Problemlerinin Gösterilmesi Üzerine İnceleme'nin girişinde, bu dönemde öğrenim gören erkeklerin zorluklarını kendisi tanımlamıştır.

    Zamanın değişkenliklerinde beni engelleyen engellerden dolayı kendimi bu cebiri öğrenmeye ve onun üzerinde yoğunlaşmaya devam etmeye adayamadım; Çünkü bizler, hayattaki dertleri, vakit uykudayken, kendilerini bir kâinatın tahkiki ve kemaline vakfetme fırsatını yakalamak olan, sayıca az, pek çok dertleri olan bir zümre dışında, bütün ilim ehlinden mahrum bırakıldık. Bilim; çünkü filozofları taklit edenlerin çoğu, doğruyu batıl ile karıştırırlar, aldatmak ve ilim uydurmaktan başka bir şey yapmazlar, ilimlerden bildiklerini maddi ve temel amaçlar dışında kullanmazlar; Bir kimsenin hakkı aradığını ve hakkı tercih ettiğini, batılı ve yalanı çürütmek için elinden geleni yaptığını, nifak ve hileyi bir yana bıraktığını görürlerse...

    Ancak Hayyam seçkin bir matematikçi ve astronomdu ve bu alıntıda anlattığı zorluklara rağmen, 25 yaşından önce Aritmetik Problemleri, müzik üzerine bir kitap ve cebir üzerine bir kitap da dahil olmak üzere birçok eser yazdı. 1070 yılında Orta Asya'nın en eski şehirlerinden biri olan Özbekistan'daki Semerkant'a taşındı. Orada Hayyam, Semerkant'ın önde gelen bir hukukçusu olan Ebu Tahir tarafından desteklendi ve bu onun en ünlü cebir eseri olan Cebir Problemlerinin Gösterilmesi Üzerine İnceleme'yi yazmasına izin verdi. Bu çalışmanın matematiksel içeriğini bu biyografide daha sonra anlatacağız.

    Selçuklu hanedanının kurucusu Tuğrul Bey, İsfahan'ı kendi topraklarının başkenti yapmış ve 1073'ten itibaren bu şehrin hükümdarı torunu Melikşah olmuştur . Hayyam'a Melikşah'tan ve veziri Nizamülmülk'ten Hayyam'dan İsfahan'a gidip orada bir Rasathane kurmasını isteyen bir davet gönderildi. Diğer önde gelen gökbilimciler de İsfahan'daki Gözlemevine getirildi ve Hayyam 18 yıl boyunca bilim adamlarına liderlik etti ve olağanüstü kalitede eserler üretti. Siyasi durumun Hayyam'a kendisini tamamen bilimsel çalışmalarına adama fırsatı verdiği bir barış dönemiydi. Bu süre zarfında Hayyam, astronomik tabloların derlenmesi çalışmalarına öncülük etti ve ayrıca 1079'da takvim reformuna katkıda bulundu..

    Melik Şah takvimi reforme etmeye karar verdiğinde, Ömer bunu yapmak için istihdam edilen sekiz alimden biriydi, sonuç Celali dönemiydi ( kralın isimlerinden biri olan Celal-üddin'den gelmektedir ) - "bir hesaplama" zaman,' diyor Gibbon, 'Julian'ı aşan ve Gregoryen stilinin doğruluğuna yaklaşan.'

    Hayyam, yılın uzunluğunu 365.24219858156 gün olarak ölçmüştür. Bu sonuca iki yorum. Birincisi, sonucu bu derece doğrulukta vermeye çalışmak inanılmaz bir güven gösterir. Artık, yılın uzunluğunun, bir kişinin yaşamı boyunca altıncı ondalık basamakta değiştiğini biliyoruz. İkincisi, olağanüstü derecede doğrudur. Karşılaştırma için 19. yüzyılın sonunda yılın uzunluğu 365.242196 idi . Bugün ise 365.242190 gün. 1092'de siyasi olaylar Hayyam'ın barışçıl varoluş dönemini sonlandırdı.

    Melikşah o yılın Kasım ayında, veziri Nizamülmülk'ün Esfahan'dan Bağdat'a giden yolda Haşhaşiler adlı terörist hareket tarafından öldürülmesinden bir ay sonra öldü. Malik-Şah'ın ikinci karısı, iki yıl boyunca hükümdarlığı devraldı, ancak Nizamülmülk ile tartıştığı için, şimdi destekledikleri desteğin geri çekildiğini gördü. Gözlemevi'ni işletmek için fon kesildi ve Hayyam'ın takvim reformu beklemeye alındı. Hayyam ayrıca, Hayyam'ın sorgulayan zihninin inanca uymadığını düşünen ortodoks Müslümanların saldırısına uğradı. Rubaiyat adlı şiirinde şunları yazmıştır :

Arthur Szyk tarafından resimlenen Omar Khayyam'ın Rubáiyát'ından ( 1940 ).

    Hayyam, tüm tarafların gözünden düşmesine rağmen Divan'da kaldı ve tekrar gözden düşmeye çalıştı. İran'daki eski yöneticileri, bayındırlık, bilim ve bursu destekleyen büyük onur adamları olarak tanımladığı bir eser yazdı.

    Melikşah'ın Horasan valisi olan üçüncü oğlu Sancar, 1118'de Selçuklu imparatorluğunun genel hükümdarı oldu . Bundan bir süre sonra Hayyam, İsfahan'dan ayrıldı ve Sanjar'ın Selçuklu imparatorluğunun başkenti yaptığı Merv'e ( şimdi Mary, Türkmenistan ) gitti. Sanjar, Hayyam'ın matematik üzerine daha fazla eser yazdığı Merv'de büyük bir İslami öğrenme merkezi yarattı.

    Kağıt Hayyam, ünlü cebir metninden önce yazılmış cebir üzerine erken bir çalışmadır. İçinde sorunu düşünüyor: -

    Çemberin çeyreği üzerindeki bir noktayı, sınır yarıçaplarından birine bu noktadan bir normal düşürüldüğünde, normalin uzunluğunun yarıçapınkine oranı, dairenin ayağı tarafından belirlenen bölümlerin oranına eşit olacak şekilde bulun.

    Hayyam, bu sorunun ikinci bir sorunu çözmeye eşdeğer olduğunu gösteriyor: -

    Hipotenüsün bir bacağın toplamı ile hipotenüs üzerindeki yüksekliğin toplamına eşit olduğu özelliğine sahip bir dik üçgen bulun.

    Bu problem Hayyam'ı kübik denklemi çözmeye yöneltti. x³ + 200x = 20x² + 2000x³ + 200x = 20x² +2000 ve dikdörtgen hiperbol ile dairenin kesişimini göz önünde bulundurarak bu kübik için pozitif bir kök buldu . Daha sonra trigonometrik tablolarda interpolasyon yoluyla yaklaşık bir sayısal çözüm bulundu. Belki daha da dikkat çekici olanı, Hayyam'ın bu küpün çözümünün konik kesitlerin kullanılmasını gerektirdiğini ve bunun cetvel ve pergel yöntemleriyle çözülemeyeceğini , bir 750 yıl daha kanıtlanamayacak bir sonuç olduğunu belirtmesidir . Hayyam ayrıca daha sonraki bir çalışmasında kübik denklemlerin çözümünün tam bir tanımını vermeyi umduğunu da yazdı.

    Fırsat olursa ve başarabilirsem, tüm bu ondört formu tüm dalları ve halleri ile ve mümkün olanla imkansız olanı nasıl ayırt edeceğimi vereceğim, böylece bu sanatta çok faydalı olan unsurları içeren bir kağıt hazırlansın.

    Gerçekten de Hayyam, kesişen konik bölümler aracılığıyla bulunan geometrik çözümlerle kübik denklemlerin tam bir sınıflandırmasını içeren Cebir Problemlerinin Gösterilmesi Üzerine İnceleme adlı böyle bir çalışma üretti. Aslında Hayyam, Yunanlıların kübik denklemler teorisi hakkında hiçbir şey bırakmadıklarını iddia ettiği ilginç bir tarihsel açıklama verir. Gerçekten de, Hayyam'ın yazdığı gibi, el-Mahani ve el -Khazin gibi daha önceki yazarların katkıları, geometrik problemleri cebirsel denklemlere çevirmekti ( el - Harezmi'nin çalışmasından önce esasen imkansız olan bir şeydi ) .. Bununla birlikte, genel bir kübik denklemler teorisini ilk tasarlayan Hayyam'ın kendisi gibi görünüyor. Hayyam şunları yazdı;

    Cebir biliminde, deneyenlerin çoğu için çözümü başarısız olan, son derece zor ön teoremlerin belirli türlerine bağlı problemlerle karşılaşılır. Kadimlere gelince, onlardan konuyla ilgili hiçbir eser bize ulaşmadı; belki çözümler aradıktan ve inceledikten sonra zorluklarını kavrayamadılar; ya da belki de soruşturmaları böyle bir incelemeyi gerektirmiyordu; ya da son olarak, varsa bu konudaki eserleri dilimize çevrilmemiştir.

    Cebir metnindeki bir diğer başarı da Hayyam'ın bir kübik denklemin birden fazla çözümü olabileceğini fark etmesidir. İki çözümü olan denklemlerin varlığını gösterdi, ancak ne yazık ki bir kübikin üç çözümü olabileceğini bulmuş görünmüyor. Bir gün yazdığında "aritmetik çözümlerin" bulunabileceğini umuyordu.

    Bilinen güçlerin yalnızca ilk üç sınıfı, yani sayı, şey ve kare olmadığı durumda, belki bizden sonra gelen bir başkası bunu bulabilir.

    "Bizden sonra gelen bir başkası" aslında 16. yüzyılda del Ferro, Tartaglia ve Ferrari'ydi. Hayyam cebir kitabında da bugün kayıp olan bir başka eserine atıfta bulunmaktadır. Kayıp eserde Hayyam Pascal üçgenini tartışır, ancak el-Karaci bu tarihten önce Pascal üçgenini tartıştığı için bunu ilk yapan o değildi . Aslında Hayyam'ın iki terimli genişlemeye ve dolayısıyla iki terimli katsayılara dayalı olarak n'inci kökleri bulmak için bir yöntem kullandığından oldukça emin olabiliriz. Bu, cebir kitabındaki aşağıdaki pasajdan çıkar.

    Hintliler, dokuz rakamlı kareler, yani 1 , 2 , 3 , vb. gibi karelerin ve ayrıca bunların birbirleriyle çarpılmasıyla oluşan ürünler, yani 2 , 3 vb. ürünleri bu yöntemlerin doğruluğunu göstermek için bir eser besteledim ve istenilen amaca götürdüğünü ispatladım. Ayrıca türleri arttırdım, yani daha önce yapılmamış olan kare-kare, dörtlü-küp, küp-küp vb. kenarlarının nasıl bulunacağını gösterdim. Bu vesileyle verdiğim ispatlar sadece Öklid'in "Elementler" inin aritmetik kısımlarına dayanan aritmetik ispatlardır.

    Öklid'in Hayyam adlı kitabının zor önermeleri üzerine yorumlarda , niyeti bu olmasa da, Öklid dışı geometriye katkıda bulunmuştur . Paralel varsayımlarını kanıtlamaya çalışırken, yanlışlıkla öklidyen olmayan geometrilerdeki şekillerin özelliklerini kanıtladı. Hayyam bu kitapta oranlar konusunda da önemli sonuçlar vermiş, Öklid'in çalışmalarını oranların çarpımını da içerecek şekilde genişletmiştir. Hayyam'ın katkısının önemi, hem Öklid'in ( ilk olarak Eudoxus tarafından önerilen ) oranların eşitliği tanımını hem de el-Mahani gibi daha önceki İslam matematikçileri tarafından önerilen oranların eşitliği tanımını incelemesidir, bu da devam eden kesirlere dayanıyordu. 

    Hayyam, iki tanımın eşdeğer olduğunu kanıtladı. Bir oranın sayı olarak kabul edilip edilemeyeceği sorusunu da sormuş, ancak soruyu cevapsız bırakmıştır. Matematik dünyasının dışında, Hayyam en iyi Edward Fitzgerald'ın 1859'da Rubaiyat adlı yaklaşık 600 kısa dört satırlık şiirin popüler çevirisinin bir sonucu olarak bilinir . Hayyam'ın şair olarak ün kazanması, bazılarının onun çok daha önemli olan bilimsel başarılarını unutmasına neden oldu. Rubaiyat'ta kullanılan biçimlerin ve ayetlerin versiyonları Hayyam'dan önce Fars edebiyatında mevcuttu ve sadece 120 kadarı vardı.ayetlerin bir kısmı kesinlikle ona isnat edilebilir. Tüm ayetler arasında en bilineni şudur: 

Eserleri :

    1. Ziyc-i Melikşahi. ( Astronomi ve takvime dair, Melikşah'a ithaf edilmiştir )
    2. Kitabün fi'l Burhan ül Sıhhat-ı Turuk ül Hind. ( Geometriye dair )
    3. Risaletün fi Berahin İl Cebr ve Mukabele. ( Cebir ve denklemlere dair )
    4. Müşkilat'ül Hisab. ( Aritmetiğe dair )
    5. İlm-i Külliyat ( Genel prensiplere dair )
    6. Newruzname ( Takvim ve yılbaşı tespitine dair )
    7. Risaletün fil İhtiyal li Marifet. ( Altın ve gümüşten yapılmış bir cisimde altın ve gümüş miktarının bilinmesine dair. Almanya Gotha kütüphanesinde bir nüshası mevcuttur. )
    8. Risaletün fi Şerhi ma Eşkele min Musaderat( Öklid'in bir probleminin çözülmesi metoduna dair, Hollanda Leiden kütüphanesinde bir nüshası vardır. F. Woepcke fransızcaya çevirmiştir. )
    9. Risaletün fi Vücud ( Felsefede ontoloji bahsine dair. Britanya kütüphanesinde bir nüshası mevcuttur. )
    10. Muhtasarun fi't Tabiiyat ( Fizik İlmine dair )
    11. Risaletün fi'l Kevn vet Teklif ( Felsefeye dair )
    12. Levazim'ül Emkine ( Meskûn yerlerin iklimi ve hava değişikliklerine dair )
    13. Fil Cevab Selaseti Mesâil ve fi Keşfil Hicab ( Üç meseleye cevap ve alemde zıtlığın zorunlu olduğuna dair )
    14. Mizan'ül Hikem ( Pırlantalı eşyaların taşlarını çıkarmadan kıymetini bulmanın yöntemine dair )
    15. Abdurrahman'el Neseviye Cevab ( Hak Teâlâ'nın alemleri yaratmasının ve insanları ibadetle yükümlü kılmasının hikmetine dair )
    16. Nizamülmülk ( Arkadaşı olan vezirin biyografisi )
    17. Eş'arı bil Arabiyye ( Arabça rûbaileri )
    18. Fil Mutayat ( İlim prensipleri )