Analitik geometri nedir ne için kullanılır?

    Analitik Geometri, cebir ve geometrinin birleşimidir. Analitik geometride, cebirsel denklemleri kullanarak geometrik şekilleri iki boyutlu bir koordinat sisteminde veya üç boyutlu bir uzayda sunmayı amaçlıyoruz. Analitik geometri, koordinat geometrisinin temel formüllerini, bir doğru ve eğri denklemlerini, eksenlerin ötelenmesi ve döndürülmesini ve üç boyutlu geometri kavramlarını içerir.

    Analitik geometrinin çeşitli alt dallarını anlayalım ve ayrıca analitik geometri ile ilgili örnekleri ve SSS'leri kontrol edelim.

Analitik Geometri Nedir?

    Analitik geometri, geometrik şekillerin iki boyutlu bir düzlemde sunulmasına ve bu şekillerin özelliklerinin öğrenilmesine yardımcı olan önemli bir matematik dalıdır. Burada, Analitik geometrinin ilk anlayışını kazanmak için koordinat düzlemi ve bir noktanın koordinatları hakkında bilgi edinmeye çalışacağız.

Koordinat Düzlemi

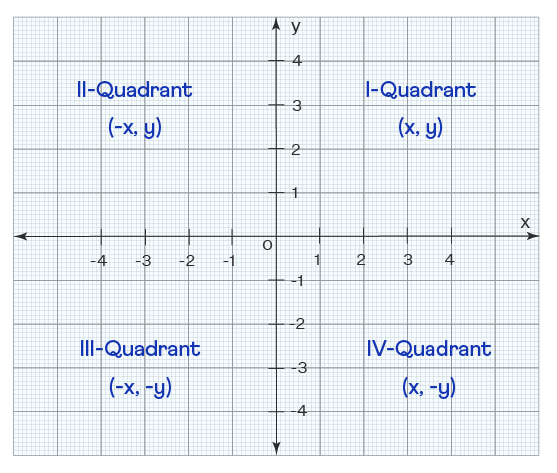
    Kartezyen düzlem, düzlem uzayını iki boyuta böler ve noktaları kolayca bulmak için kullanışlıdır. Koordinat düzlemi olarak da adlandırılır. Koordinat düzleminin iki ekseni yatay x ekseni ve dikey y eksenidir. Bu koordinat eksenleri düzlemi dört çeyreğe böler ve bu eksenlerin kesişme noktası orijindir (0, 0). Ayrıca, koordinat düzlemindeki herhangi bir nokta, x eksenine göre noktanın konumu ve y değeri, y eksenine göre noktanın konumu olduğu bir nokta (x, y) ile ifade edilir.

    Koordinat düzleminin dört çeyreğinde temsil edilen noktanın özellikleri şunlardır:

• Orijin O, x ekseni ile y ekseninin kesişme noktasıdır ve (0, 0) koordinatlarına sahiptir.
• Orijin O'nun sağındaki x ekseni pozitif x eksenidir ve orijinin solundaki O negatif x eksenidir. Ayrıca, orijin O'nun üzerindeki y ekseni pozitif y eksenidir ve orijin O'nun altındaki negatif y eksenidir.
• İlk çeyrekte (x, y) temsil edilen nokta hem pozitif değerlere sahiptir hem de pozitif x ekseni ve pozitif y ekseni referans alınarak çizilir.
• İkinci çeyrekte temsil edilen nokta (-x, y), negatif x ekseni ve pozitif y ekseni referans alınarak çizilir.
• Üçüncü çeyrekte (-x, -y) temsil edilen nokta, negatif x ekseni ve negatif y ekseni referans alınarak çizilir.
• Dördüncü çeyrekte (x, -y) temsil edilen nokta, pozitif x ekseni ve negatif y ekseni referans alınarak çizilir.

Bir Noktanın Koordinatları

    Koordinatlar, uzayda bir noktanın yerini belirlemeye yardımcı olan bir adrestir. İki boyutlu bir uzay için, bir noktanın koordinatları (x, y) 'dir. Burada bu iki önemli terimi not edelim.

• Apsis: (x, y) noktasındaki x değeridir ve bu noktanın x ekseni boyunca orijinden uzaklığıdır
• Ordinasyon: (x, y) noktasındaki y değeridir ve noktanın y eksenine paralel olan x eksenine dik uzaklığıdır.

    Bir noktanın koordinatları, mesafeyi, orta noktayı, bir doğrunun eğimini, bir doğrunun denklemini bulmak için çok sayıda işlem yapmak için kullanışlıdır.

Analitik Geometri - Eksenlerin Ötelenmesi ve Döndürülmesi

    Analitik geometrideki koordinat eksenleri, yeni eksenler eski eksenlere paralel olacak şekilde eksenlerin hareket ettirilmesiyle çevrilebilir. Ayrıca koordinat eksenleri, x eksenine göre orijin etrafında bir açıyla da döndürülebilir. Aşağıdaki cümlelerde eksenlerin çevirisi ve dönüşü hakkında bize daha fazla bilgi veriyor.

Axes sözcüğünün çevirisi

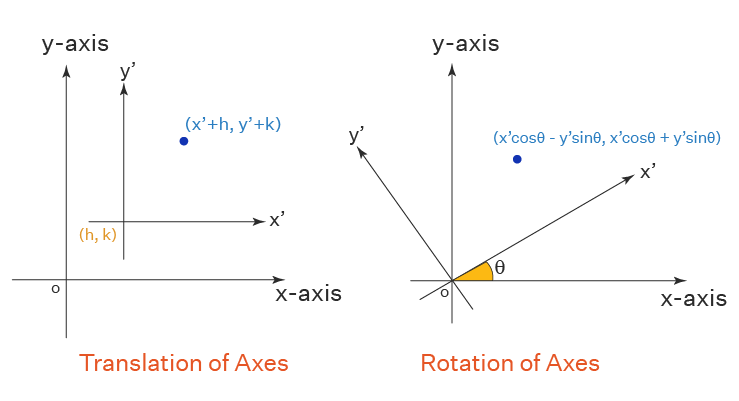
    Orijini O olan verilen koordinat eksenleri, bir noktanın koordinatlarını (x, y) olarak gösterir. Burada orijini eski koordinat eksenlerine göre (h, k) noktasında bulunan yeni bir orijin O'ya aktarıyoruz. Yeni koordinat eksenleri, yeni eksenler eski eksenlere paralel olacak şekilde çevrilir. Bir noktanın koordinatları (x, y)'den (x' + h, y' + k) ye dönüşür. Eski eksenlere göre bir doğrunun veya eğrinin herhangi bir denklemi, denklemde (x + h, y + k) ile basitçe (x, y) değiştirilerek yeni eksenlere göre kolayca değiştirilebilir.

Eksenlerin Dönüşü

    Ox ve oy koordinat eksenleri, yeni ox' ve oy' eksenlerini elde etmek için saat yönünün tersine bir θ açısıyla döndürülür. Bir noktanın eski eksenlere göre koordinatları (x, y) ve dönüşte yeni eksenlere göre koordinatlar (x', y') olur. Ayrıca, (x', y') yü (xCosθy -Sinθ, xSinθ + ycosθ) olarak değiştirerek eski koordinatları geri alabiliriz.

Koordinat Düzleminde Analitik Geometri Formülleri

    Koordinat geometrisinin formülleri, koordinat eksenlerinde temsil edilen çizgilerin ve şekillerin çeşitli özelliklerinin uygun bir şekilde kanıtlanmasına yardımcı olur. Koordinat geometrisinin önemli formülleri uzaklık formülü, eğim formülü, orta nokta formülü ve kesit formülüdür. Aşağıdaki paragraflardaki formüllerin her biri hakkında bize daha fazla bilgi veriyor.

Uzaklık Formülü

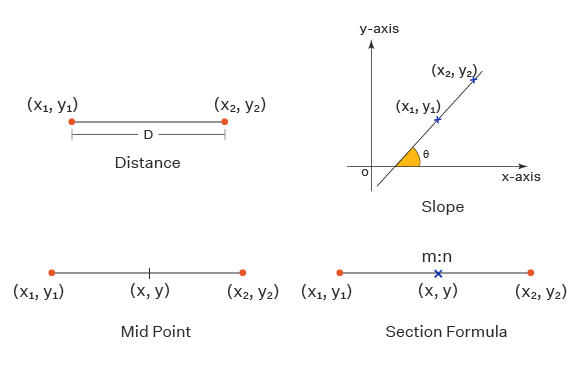
    İki nokta arasındaki mesafe (x₁, y₁) ve (x₂, y₂) x koordinatlarının farkının karelerinin toplamının kareköküne ve verilen iki noktanın y koordinatlarının farkına eşittir. Verilen iki nokta arasındaki mesafeyi bulma formülü aşağıdaki gibidir.

    D = √(x₂ − x₁)² + (y₂ − y₁)²

Eğim Formülü

    Bir doğrunun eğimi, doğrunun eğimidir. Eğim, pozitif x ekseni ile doğrunun yaptığı açıdan veya doğru üzerindeki herhangi iki nokta alınarak hesaplanabilir. Pozitif x ekseni ile θ açısında eğimli bir doğrunun eğimi m = Tanθ'dır. İki noktayı birleştiren bir doğrunun eğimi (x₁, y₁) ve (x₂, y₂) şuna eşittir m = (y₂ − y₁) / (x₂ − x₁).

Orta Nokta Formülü

    Noktaları birleştiren doğrunun orta noktasını bulma formülü (x₁, y₁) ve (x₂, y₂) apsisi verilen iki noktanın x değerlerinin ortalaması olan yeni bir noktadır ve ordinat, verilen iki noktanın y değerlerinin ortalamasıdır. Orta nokta, iki noktayı birleştiren çizgi üzerinde yer alır ve tam olarak iki nokta arasında bulunur.

    (x, y) = (x₁+x₂ / 2 , y₁+y₂ / 2)

Koordinat Geometrisinde Kesit Formülü

    Kesit formülü, noktaları birleştiren doğru parçasını bölen bir noktanın koordinatlarını bulmak için kullanışlıdır (x₁, y₁) ve (x₂, y₂) oranında m:n. Verilen iki noktayı bölen nokta, iki noktayı birleştiren doğru üzerinde yer alır ve iki nokta arasında veya bu iki noktanın ötesinde bulunur. Verilen iki nokta için bölüm formülünün ifadesi ve oranı aşağıdaki gibidir.

    (x, y) = (mx₂+nx₁ / m+n , my₂+ny₁ / m+n)

Analitik Geometri - Bir Doğrunun Denklemleri

    Koordinat düzlemindeki noktalar kümesi bir çizgiyi temsil eder. Analitik geometride, bir doğrunun denklemi tüm bu nokta kümesini tanımlamaya yardımcı olur. Doğrunun bir denklemini oluşturmanın yaklaşık beş temel farklı biçimi vardır. Bir doğrunun denkleminin farklı biçimleri aşağıdaki gibidir.

• Nokta Eğim Formu
• İki Nokta Formu
• Eğim - kesişim formu
• Kesişim formu
• Normal form

    Bir çizgi denkleminin bu biçimlerinin her biri hakkında daha fazla bilgi edinmeye çalışalım.

Nokta - Eğim Formu

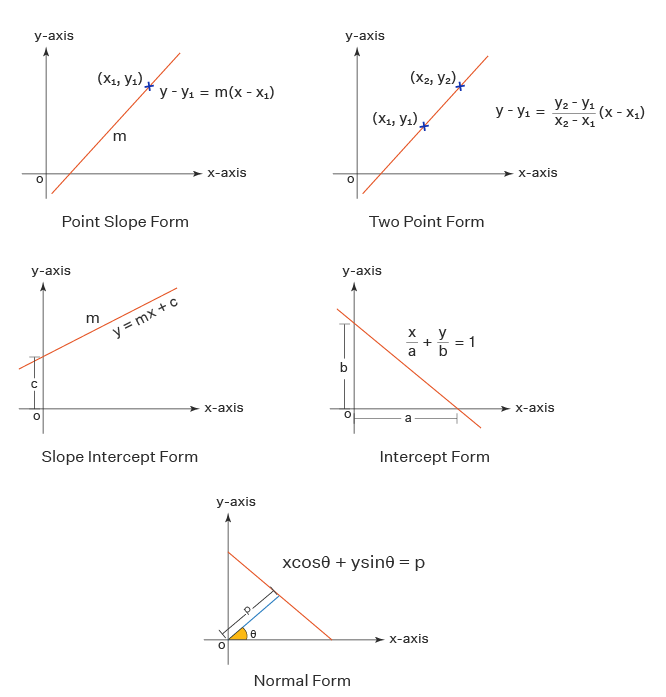
    Bir doğrunun denkleminin nokta - eğim formu, doğru üzerinde bir nokta ve doğrunun eğimini gerektirir. Çizgi üzerinde atıfta bulunulan nokta (x₁, y₁) ve doğrunun eğimi m'dir. Nokta sayısal bir değerdir ve x koordinatını ve noktanın y koordinatını temsil eder ve m doğrusunun eğimi, pozitif x ekseni ile doğrunun eğimidir. Bir doğrunun denkleminin nokta - eğim formu (y - y₁) = m(x - x₁).

İki Nokta Formu

    Bir doğrunun denkleminin iki noktalı formu, bir doğrunun denkleminin nokta - eğim formunun daha ileri bir açıklamasıdır. Bir doğrunun denkleminin nokta - eğim biçiminde, eğim m = (y₂ - y₁)/(x₂ - x₁) bir doğrunun denkleminin iki noktalı biçimini oluşturmak için ikame edilir. İki noktadan geçen bir doğrunun denklemi (x₁, y₁) ve (x₂, y₂) aşağıdaki gibidir.

    (y − y₁) = (y₂ − y₁)/(x₂ − x₁)  (x − x₁)

Eğim Kesişim Formu

    Bir doğrunun eğim - kesişim formu y = mx + c dir. Burada m doğrunun eğimidir ve 'c' doğrunun y-kesişim noktasıdır. Bu çizgi y eksenini (0, c) noktasında keser ve c, y eksenindeki bu noktanın orijinden uzaklığıdır. Bir doğrunun denkleminin eğim - kesişim formu önemli bir formdur ve matematik ve mühendisliğin farklı konularında harika uygulamalara sahiptir.
    y = mx + c

Kesişme Formu

    Kesişim formundaki bir doğrunun denklemi, x-kesişim noktası 'a' ve y-kesişim noktası 'b' ile oluşturulur. Doğru, x eksenini (a, 0) noktasında ve y eksenini (0, b) noktasında keser ve a, b, bu noktaların orijinden ilgili mesafeleridir. Ayrıca, bu iki nokta, bir çizgi denkleminin iki noktalı formunda ikame edilebilir ve çizgi denkleminin bu kesişme biçimini elde etmek için basitleştirilebilir. Bu kesişim formu, çizginin x eksenini ve y eksenini orijinden kestiği mesafeyi açıklar.
    x/a + y/b = 1

Normal Form

    Bir çizginin denkleminin normal şekli, orijinden geçen çizgiye dik olana dayanır. Verilen çizgiye dik olan ve orijinden geçen çizgiye normal denir. Burada normalin uzunluğu 'p' ve bu normalin pozitif x ekseni ile yaptığı açı 'θ' dir. Bir doğrunun denkleminin normal formunun denklemi xcosθ + ysinθ = p dir.

Analitik Geometri - Konik Kesit

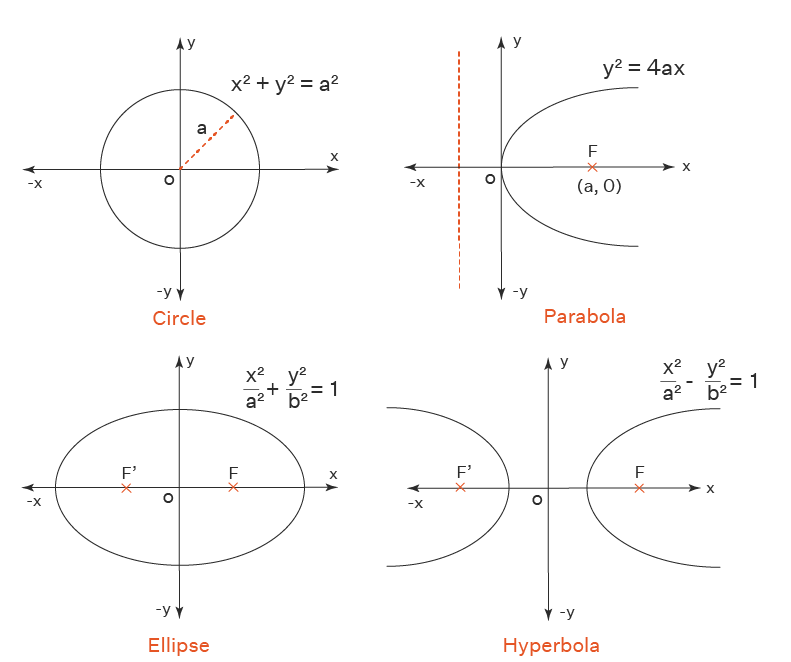
    Analitik geometrideki konik kesit, eğri çizgilerden oluşturulmuş eğrileri temsil eder ve odak adı verilen sabit bir nokta ve directrix adı verilen sabit çizgi referans alınarak tanımlanmıştır. Önemli konikler daire, parabol, elips ve hiperboldür. Farklı koniklerin standart denklem şekli aşağıdaki gibidir.

• Daire: x²+y² = a²
• Parabol: y² = 4ax olduğunda a>0
• Elips: x²/a² + y²/b² = 1
• Hiperbol: x²/a² - y²/b² = 1

Daire

    Dairenin bir merkezi ve yarıçapı vardır. Bir daire, bir noktanın yerini, merkez adı verilen sabit bir noktadan uzaklığı, yarıçap adı verilen sabit bir değere eşit olacak şekilde temsil eder. Merkezi (h, k) olan ve yarıçapı r birim olan bir dairenin genel denklemi (x - h)² + (y - k)² = r². Ayrıca, merkezi (0, 0) olan ve 'a' birimlerinin yarıçapı x²+y² = a² olan bir dairenin standart denklemi.

Parabol

    Bir parabol, eğri üzerindeki bir noktanın sabit bir noktadan ve sabit bir çizgiden eşit uzaklıkta olduğu bir eğri denklemini ifade eder. Sabit noktaya parabolün odağı, sabit çizgiye ise parabolün directrix'i denir. Belirli bir noktadan ( odak ) ve belirli bir çizgiden ( directrix ) eşit uzaklıkta olan herhangi bir noktanın lokusuna parabol denir. Bir parabolün genel denklemi: y = a(xh)² + k veya x = a(yk)² +h, burada (h, k) tepe noktasını gösterir. Düzenli bir parabolün standart denklemi y² = 4ax'tır.   

Elips

    Matematikte bir elips, sabit bir noktadan uzaklığı, 1'den küçük olan sabit bir çizgiden uzaklığına sabit bir 'e' oranına sahip olacak şekilde bir düzlem noktasının yeridir. Sabit noktaya odak denir ve sabit oran olan S ile gösterilir e eksantrikliktir ve sabit çizgiye elipsin directrix'i (d) denir. Ayrıca, bir elips, iki sabit noktadan uzaklıklarının toplamı sabit bir değer olan bir noktanın yeridir. İki sabit noktaya elipsin odakları denir. Bir elipsin standart denklemi x²/a² + y²/b² = 1

Hiperbol

    Hiperbol, iki odaktan uzaklık farkı sabit bir değer olan bir dizi noktadır. Bu fark, daha uzak odağa olan mesafeden ve ardından daha yakın odağa olan mesafeden alınır. Bir nokta için P(x, y). hiperbolde ve iki odak F, F' için, hiperbolün lokusu PF - PF' = 2a dır. Denklem x²/a² − y²/b² = 1 bir hiperbol denkleminin standart biçimini temsil eder. Burada x ekseni hiperbolün enine eksenidir ve y ekseni hiperbolün eşlenik eksenidir.

Üç Boyutlu Uzayda Analitik Geometri

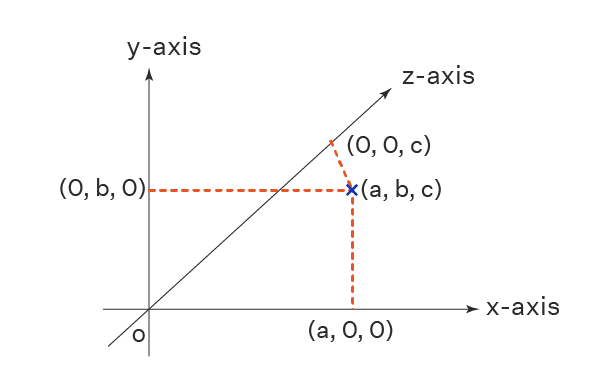
    Çevremizdeki uzay, sırasıyla x ekseni, y ekseni ve z ekseni yardımıyla üç boyutlu bir uzay olarak görselleştirilebilir. Bu, sırasıyla bir doğrunun ve bir düzlemin denklemlerini sunmak için kullanışlıdır.

Yön Oranları ve Yön Kosinüsleri

    Orijinden geçen ve (a, b, c) noktasından geçen doğrunun yön oranları sırasıyla a, b, c olur. Ayrıca, bu çizgi α, β bir açı yapar γ x ekseni, y ekseni, y ekseni, o zaman Cosα, Cosβ, Cosγ doğrunun yön kosinüsleri olarak adlandırılır.

    Bu yön kosinüsleri l, m, n ile temsil edilir ve l = ± a/√a²+b²+c², m = ± b/√a²+b²+c², n = ± c/√a²+b²+c².

Bir Doğrunun Denklemi

    Bir doğrunun denklemi, aşağıdaki formüller kullanılarak iki şekilde hesaplanabilir.

1. Belirli bir noktadan geçen bir doğrunun denklemi →a ve vektöre paralel →b dir →r. = →a + λ →b.
2. Verilen iki noktadan geçen bir doğrunun denklemi →a ve →b dir →r. = →a + λ(→b − →a).

    Not: '→' işareti gösterdiği harfin üzerine yazılır.

Bir Düzlemin Denklemi

    Verilen girdi değerlerine dayalı olarak bir düzlemin denklemini yazmanın dört farklı yolu vardır.

1. Orijinden d birim uzaklıktaki düzlem denklemi ve normal bir n'ye sahip olan denklem →r.^n = d.
2. Bir noktadan geçen bir düzlemin denklemi →a ve normal bir vektöre sahip olmak →N dir (→r − →a).→N = 0.
3. Üç vektör noktasından geçen bir düzlemin denklemi →a, →b ve →c dir (→r − →a).[(→b − →a) × (→c − →a)] = 0.
4. Normal vektörlere sahip iki düzlemden geçen bir düzlemin denklemi →n₁, →n₂ ve orijinden uzaklıklar d₁, d₂ sırasıyla →r.(→n₁ + λ→n₂) = d₁ + λd₂.

    Not: '→' işareti gösterdiği harfin üzerine yazılır.

İki Çizgi ve İki Düzlem Arasındaki Açı

    İki çizgi ve iki düzlem arasındaki açı, aşağıdaki formül seti kullanılarak hesaplanabilir.

1. Yön oranlarına sahip iki doğru arasındaki açı a₁, b₁, c₁ ve a₂, b₂, c₂ sırasıyla Cosθ = |∣ a₁.a₂ + b₁.b₂ + c₁.c₂ / √₁a² + ₁b² + ₁c² . √₂a² + ₂b² + ₂c² ∣|.
2. İki düzlem arasındaki açı A₁x + B₁y + C₁Z + D₁ = 0, A₂x + B₂y + C₂Z + D₂ = 0 dir Cosθ = |∣ A₁.A₂ + B₁.B₂ + C₁.C₂ / √₁A² + ₁B² + ₁C² . √₂A² + ₂B² + ₂C² ∣|.

Analitik Geometri Örnekleri

1. Örnek 1: Analitik geometride, sırasıyla 5 birimlik x-kesişim noktasına ve 6 birimlik y-kesişim noktasına sahip bir doğrunun denklemini bulun.

   Çözüm:

   X ekseninin verilen kesişimleri a = 5 ve y ekseninin b = 6 dır.

   Düz çizginin gerekli denklemi x/a + y/b = 1 dir.

   x/5 + y/6 = 1

   6x + 5y = 30

   Bu nedenle, doğrunun gerekli denklemi 6x + 5y = 30 dur.

2. Örnek 2: (4, -3, 2) ve (2, 1, 5) noktalarını birleştiren doğrunun orta noktasının koordinatlarını bulun. Üç boyutlu uzayda analitik geometrinin orta nokta formülünü kullanın.

   Çözüm:

   Verilen puanlar (4, -3, 2) ve (2, 1, 5) tir.

   Orta nokta formülünü kullanarak MP = (x₁+x₂ / 2 , y₁+y₂ / 2 , z₁+z₂ / 2)

   MP = (4+2 / 2 , (−3)+1 / 2 , 2+5 / 2)

   MP = (3, -1, 7/2).

   Bu nedenle orta noktanın koordinatları (3, -1, 7/2) dir.

Analitik Geometri Alıştırma Soruları

İşte pratik yapmanız için birkaç aktivite.

1. Aşağıdakilerden hangisi Analitik Geometrinin bir parçası değildir?

   • a. Düzlem Geometrisi
   • b. Üç Boyutlu Geometri
   • c. Koordinat Geometrisi

 

2. Aşağıdakilerden hangisi analitik geometride üç boyutlu çerçevede iki nokta arasındaki mesafeyi bulma ifadesini ifade eder?

   • a. √(x₂+x₁)²+(y₂+y₁)²+(z₂+z₁)²
   • b. √(x₂-x₁)²+(y₂-y₁)²+(z₂-z₁)²

    Cevaplar yazının altındadır.

Sıkça Sorulan Sorular – SSS

1. Analitik geometri nedir?

    Analitik geometri, noktanın düzlem üzerindeki konumunun Koordinatlar adı verilen sıralı bir sayı çifti kullanılarak belirlendiği Cebir dalıdır. Bir düzlemdeki noktalar, çizgiler vb. gibi farklı nesneleri modellemek için kullanılır. Analitik geometri bazen Koordinat geometrisi veya Kartezyen geometri olarak adlandırılır.

2. Üç boyutlu geometri analitik geometrinin bir parçası mıdır?

    Üç boyutlu geometri, analitik geometrinin bir parçasıdır. Üç boyutlu uzaydaki çizgiler veya düzlemler, analitik geometri kavramları kullanılarak temsil edilir.

3. Analitik geometrinin temel prensibi nedir?

    Analitik geometrinin temel prensibi, nokta, çizgi, eğri vb. geometrik şekillerin koordinat sistemindeki konumunu ve boyutunu tanımlamaktır.

4. Analitik geometrinin babası kimdir?

    Rene Descartes genellikle Analitik Geometrinin babası olarak kabul edilir.

5. Analitik geometri ne için kullanılır?

    Analitik geometri fizik, bilim ve mühendislik, uzay ve havacılık gibi farklı alanlarda kullanılmaktadır. Ayrıca cebir, diferansiyeller, ayrık ve hesaplamalı geometri gibi en gelişmiş geometri alanlarının temelidir.

6. Analitik geometrinin konuları nelerdir?

    Analitik geometrinin konuları arasında koordinat geometrisi, üç boyutlu geometri, vektörler yer almaktadır. Burada ayrıca eksenlerin ötelenmesi ve döndürülmesi, çizgi denklemi ve eğri denklemi, üç boyutlu geometride bir çizgi ve düzlem denklemi konularını da içerir.

7. Analitik geometri nasıl yapılır?

    Analitik geometri, denklem çözmenin cebirsel kavramları kullanılarak çözülür. Burada, cebirsel kavramlar kullanılarak daha da çözülen geometrik şekilleri temsil etmek için temel mesafe formülünü, orta nokta formülünü, bölüm formülünü, çizgi denklemini ve eğri formülünü kullanıyoruz.

8. Analitik geometrinin koordinat geometrisinden farkı nedir?

    Koordinat geometrisi, analitik geometrinin bir alt konusudur. Analitik geometri ayrıca üç boyutlu geometri ve vektörler konularını da içerir.

    Cevaplar: 1a 2b