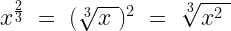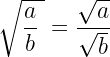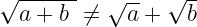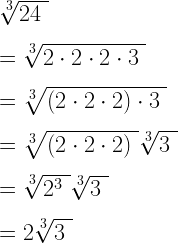Kökler ve Rasyonel Üsler

    Toplama ve çarpma değişmeli olsa da, üs değişmeli değildir: tabandaki değeri üsteki değerle değiştirmek farklı bir sonuç üretecektir ( tabii ki aynı değer olmadıkça ): 

    2³ ≠ 3²

    Bu nedenle, üstel ifadeler içeren denklemleri çözmek için iki farklı ters fonksiyona ihtiyaç vardır: 

    – kökler, üsleri geri almak için – logaritmalar, tabanları geri almak için. 

    Toplama fonksiyonunun birçok versiyonu ( eklemek isteyebileceğiniz her sayı için bir tane ) ve ‘logaritma’ fonksiyonunun birçok versiyonu ( her biri farklı bir tabana sahip ) olduğu gibi, ‘kök’ fonksiyonunun da birçok versiyonu vardır: geri alınacak her üs değeri için bir tane. 

Gösterim

    Kökün sembolü √ 'dir ve ‘radikal’ olarak adlandırılır. Solda bir tür onay işaretinden ve ardından okuyucunun kökün tam olarak neye uygulandığını bilmesini sağlamak için bir gruplama sembolü ( parantez gibi ) görevi gören ‘vinculum’ adı verilen yatay bir çizgiden oluşur. Radikalin altındaki ifadeye ‘radikand’ denir. Kökler, bize geri aldıkları üssü söyleyen bir ‘indeks’ ile etiketlenebilir ( veya etiketlenmeyebilir ). Dizin, radikalin solundaki çentiğin üzerinde görünür.

    Yukarıdaki ifadede, "x" radikanddır. İndeksi 3 olan bir radikalin altındadır ve "x'in küp kökü" olarak okunur. 

    Karekökler ( indeksi 2 olan kökler ) diğer köklerin çoğundan daha sık kullanılır, bu nedenle indeks atlanarak bunların gösterimi biraz basitleştirilmiştir: 

    Herhangi bir dizin gösterilmezse, dizinin 2 ( karekök ) olduğu varsayılır. 

Ters Fonksiyonlar Olarak Kökler

    "Karekök", 2'nin üssünü geri alır. Geometrik terimlerle, bir karenin alanının karekökü size karenin dört kenarının her birinin uzunluğunu söyler: 

    Yukarıdaki denklemde, "16" yarıçaptır. İndeksi 2 olan bir radikalin altında. Alanı 16 olan bir karenin kenarları 4 uzunluğundadır.

    "Dört kare" nin karekökü dörttür. Başka bir deyişle, ters fonksiyonların birbirine uygulandığını görürseniz, basitleştirmeden önce en içteki ifadeyi değerlendirmenize gerek yoktur:

    Bir "küp kök", 3'ün üssünü geri alır: 

    Bir kökün indisi bir üssün değeriyle eşleştiğinde, bunlar ters fonksiyonlardır. Biri diğerini "geri alır":

    İki ters fonksiyonun ortaya çıkma sırası önemli değildir. Yukarıdaki iki örnekte gösterildiği gibi, "yolda" başka hiçbir şey olmadığı sürece her zaman birbirlerini geri alacaklardır. Durumun böyle olmadığı durumlara ilişkin bazı örnekler aşağıdadır. Her birinin "yolunda" olan bir şeyi vardır (3), bu da onları "tersine uygulanan bir işlevin" örnekleri olmaktan alıkoyar:

    Yukarıdakilerden bazıları Kök Yasaları ( aşağıda tartışılacak ) kullanılarak daha da basitleştirilebilirken, yukarıda göründükleri gibi "ters fonksiyonlar birbirini iptal eder" kavramı kullanılarak basitleştirilemezler. 

Rasyonel Üsler Olarak Kökler

    Çıkarma işleminin bir negatifin toplanması olarak yeniden yazılabilmesi veya bölmenin karşılıklı ile çarpma olarak yeniden yazılabilmesi gibi, bir kök de rasyonel üs ( iki tamsayının oranı olan bir üs ) olarak yeniden yazılabilir. Aşağıdaki doğru ifadeyi göz önünde bulundurun:

    Beşin karesi için de benzer bir durum kurarsak, ancak kendimize kareyi geri almak için bir üssü nasıl kullanabileceğimizi sorarsak, şunu elde ederiz: 

    Üslü sayılar yasaları bize, üstel bir ifadeyi bir kuvvete yükselttiğimizde, kuvvetleri çarpmamız gerektiğini söyler, böylece önceki ifadeyi şu şekilde yeniden yazabiliriz: 

    Yukarıdaki ifadenin doğru olması için, iki üs birbirine eşit olmalıdır: 

    Başka bir deyişle, yarım kuvvete yükseltilen bir karesi olan bir nicelik, birin üssü ile sonuçlanacaktır, bu da hiç üs olmamasıyla aynıdır. Bir karekök almak, yarım kuvvete yükseltmekle aynı etkiye sahiptir. Bir küp kök almak ( 3 indeksi ), üçte bir kuvvetine yükseltmekle aynı etkiye sahiptir.

    Kökler kesirli üslere dönüştürüldüğünde ifadeleri değiştirmek genellikle daha kolaydır. Aşağıda, bir ifadenin yeniden yazılabileceği çeşitli yollar gösterilmektedir:

    Rasyonel bir üs ile karşılaştığınızda, pay kuvvet, payda ise köktür. Gücü ve kökü hangi sırayla değerlendirdiğiniz önemli değil; Her iki sipariş de aynı sonucu verecektir:

Köklerin Kanunları

    Kökler kesirli üsler olarak ifade edilebildiğinden, üsler yasaları kökler için de geçerlidir. Bir üs bir ürün veya bölüm üzerinde dağıtılabildiğinden, bir kök de olabilir. Bu kuralların her birinin soldan sağa veya sağdan sola kullanılabileceğini unutmayın.

    Bir ürünün kökü, köklerin ürünüdür. 

    Bir bölümün kökü, köklerin bölümüdür. 

    Üslerin toplamlar veya farklar üzerinde dağılmadığını ve dolayısıyla kesirli üslerin veya köklerin de dağılmadığını hatırlayın. Birçok kişinin ifadeleri eşdeğer OLMAYAN şekillerde yeniden yazma eğiliminde olduğu aşağıdaki durumlara dikkat edin:

Kökleri Basitleştirmek

    4 veya 25 gibi sayıların karekökünü güvenle okuyan birçok öğrenci, başlangıçta daha az kolay sayıların basitleştirilmiş köklerini zor bulabilir. İki yaklaşım süreci basitleştirmeye yardımcı olur:

1. Sorunu küçük parçalara ayırın ve her seferinde bir parça üzerinde çalışın. 
2. Ters fonksiyonlar birbirini geri alır, en içteki fonksiyonun içindekini "serbest bırakır". 

    Kökleri basitleştirmeyi öğrenmek, genellikle öğrencilerin bir fonksiyonun doğasına ters olarak güvenmeye zorlandıkları ilk durumdur. Tamamen ezberci bir yaklaşım tüm problemlerde işe yaramaz. Önceki işlemler veya işlevler ters olarak açıklanmış olsa da, öğrenciler genellikle bu tür problemleri ezberci yollarla çözmeye devam etmeyi başardılar. Bu nedenle, iki işlevin birbirini ilk kez nasıl "geri alabileceği" ile boğuşurken ekstra bir sabır ve azim yardımı yararlıdır.

    Bir kökü basitleştirmek için, kökün altındaki ifadeyi asal çarpanların bir ürünü olarak yeniden yazmak çok yararlıdır. Ortaokuldayken asal çarpanlarına ayırma işlemini kullanarak bir sayıyı yeniden yazma pratiği yapan herkes şimdi faydalı olacaktır:

    Karekök kareyi geri alır, bu nedenle karekökü basitleştirmek için iki kez görünen faktörleri bulmanız gerekir. Her bir miktarı asal çarpanlarına ayırma işleminde yeniden yazarak, yukarıda gösterildiği gibi tekrarlanan faktörleri bulmayı kolaylaştırırsınız. Faktör çiftleri tanımlandıktan sonra, Kök Yasaları kullanılarak ayrı bir radikallere ayrılabilirler, daha sonra bir karekökün bir kareyi çözdüğünü kabul ederek basitleştirilebilirler.

    Tam olarak aynı işlem HERHANGİ bir kök için de geçerlidir, ancak aynı faktör çiftlerini aramak yerine, kökün indeksi size bir faktörün basitleştirilebilmesi için kaç örneğinin gerekli olduğunu söyler: 

    İfadeler daha da karmaşık hale geldikçe, aynı süreç uygulanmaya devam eder: 

    Çoğu matematik probleminde olduğu gibi, cevaba ulaşmanın birden fazla geçerli yolu vardır... Ve bazı yollar diğerlerinden daha verimli olacaktır. Ancak, kavramlara hakim olana ve en rahat olduğunuz yaklaşımı kullanarak doğru bir cevaba ulaşabileceğinizden emin olana kadar verimlilik konusunda endişelenmeyin. Bu nedenle, örneğin, yukarıdaki sorun aşağıdaki gibi basitleştirilebilir:

    veya rasyonel üsleri kullanarak: