Sıfır Faktöriyel Neden Bire Eşittir?
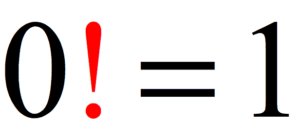
Sıfır faktöriyel, içinde hiçbir değer olmayan bir veri kümesini düzenleme yollarının sayısı için matematiksel bir ifadedir; bu, bire eşittir. Genel olarak, bir sayının faktöriyeli , sayının kendisinden küçük ama sıfırdan büyük her sayı ile çarpıldığı bir çarpma ifadesi yazmanın kestirme bir yoludur. 4! = 24, örneğin, 4 x 3 x 2 x 1 = 24 yazmakla aynıdır, ancak aynı denklemi ifade etmek için faktöriyel sayının (dört) sağında bir ünlem işareti kullanılır.
Bu örneklerden, birden büyük veya ona eşit herhangi bir tam sayının faktöriyelinin nasıl hesaplanacağı oldukça açıktır , ancak sıfırla çarpılan herhangi bir şeyin sıfıra eşit olduğu matematiksel kuralına rağmen, sıfır faktöriyelin değeri neden birdir?
Faktöriyelin tanımı 0! = 1. Bu, genellikle bu denklemi ilk gördüklerinde insanların kafasını karıştırır, ancak sıfır faktöriyelin tanımına, permütasyonlarına ve formüllerine baktığınızda bunun neden mantıklı olduğunu aşağıdaki örneklerde göreceğiz.
Sıfır Faktöriyelin Tanımı
Sıfır faktöriyelin bire eşit olmasının ilk nedeni, tanımın böyle olması gerektiğini söylüyor olmasıdır, ki bu matematiksel olarak doğru bir açıklamadır (biraz tatmin edici değilse). Yine de, bir faktöriyelin tanımının, orijinal sayıya eşit veya daha az değere sahip tüm tam sayıların çarpımı olduğu unutulmamalıdır - başka bir deyişle, faktöriyel, bu sayıdan küçük veya ona eşit sayılarla mümkün olan kombinasyonların sayısıdır.
Sıfırın kendisinden daha küçük bir sayısı olmadığı, ancak yine de kendi içinde bir sayı olduğu için, bu veri kümesinin nasıl düzenlenebileceğinin yalnızca bir olası kombinasyonu vardır: olamaz. Bu hala onu düzenlemenin bir yolu olarak sayılır, bu nedenle tanım gereği sıfır faktöriyel bire eşittir, tıpkı 1 gibi! bire eşittir çünkü bu veri kümesinin yalnızca tek bir olası düzenlemesi vardır.
Bunun matematiksel olarak nasıl bir anlam ifade ettiğini daha iyi anlamak için, bunun gibi faktöriyellerin bir dizideki olası bilgi sıralarını belirlemek için kullanıldığını, ayrıca permütasyon olarak da bilindiğini ve içinde hiçbir değer olmamasına rağmen bunun anlaşılmasında yararlı olabileceğini belirtmek önemlidir. boş veya sıfır küme, yine de kümenin düzenlenmesinin bir yolu vardır.
Permütasyonlar ve Faktöriyeller
Bir permütasyon , bir kümedeki öğelerin belirli, benzersiz bir sırasıdır. Örneğin, {1, 2, 3} kümesinin üç eleman içeren altı permütasyonu vardır, çünkü bu elemanları aşağıdaki altı yolla yazabiliriz:
- 1, 2, 3
- 1, 3, 2
- 2, 3, 1
- 2, 1, 3
- 3, 2, 1
- 3, 1, 2
Bu gerçeği denklem 3 ile de ifade edebiliriz! = 6, permütasyonların tam setinin faktöriyel bir temsilidir. Benzer şekilde 4 tane var! = Dört elemanlı ve 5'li bir kümenin 24 permütasyonu! = Beş elemanlı bir kümenin 120 permütasyonu. Bu yüzden faktöriyel hakkında düşünmenin alternatif bir yolu, n'nin doğal bir sayı olmasına izin vermek ve n ! n elemanlı bir küme için permütasyon sayısıdır .
Faktöriyel hakkında bu şekilde düşünerek, birkaç örneğe daha bakalım. İki elemanlı bir kümenin iki permütasyonu vardır : {a, b} a, b veya b, a olarak düzenlenebilir. Bu 2'ye karşılık gelir! = 2. Tek elemanlı bir kümenin tek bir permütasyonu vardır, çünkü {1} kümesindeki 1 elemanı sadece tek bir şekilde sıralanabilir.
Bu bizi sıfır faktöriyeline getiriyor. Sıfır elemanlı kümeye boş küme denir . Sıfır faktöriyelin değerini bulmak için, "Elementi olmayan bir kümeyi kaç farklı şekilde sıralayabiliriz?" diye sorarız. Burada düşüncemizi biraz genişletmemiz gerekiyor. Sıraya koymak için hiçbir şey olmasa da, bunu yapmanın bir yolu var. Böylece 0'ımız var! = 1.
Formüller ve Diğer Doğrulamalar
0 tanımının bir başka nedeni! = 1, permütasyonlar ve kombinasyonlar için kullandığımız formüllerle ilgilidir. Bu, sıfır faktöriyelin neden bir olduğunu açıklamaz, ancak neden 0'ın ayarlandığını gösterir! = 1 iyi bir fikirdir.
Kombinasyon, bir kümenin elemanlarının sıra gözetmeksizin gruplandırılmasıdır. Örneğin, {1, 2, 3} kümesini düşünün, burada üç öğenin hepsinden oluşan bir kombinasyon vardır. Bu öğeleri nasıl düzenlersek düzenleyelim, aynı kombinasyonla sonuçlanırız.
Formülü , bir seferde üç öğenin kombinasyonu ile kombinasyonlar için kullanıyoruz ve 1 = C (3, 3) = 3!/(3! 0!) olduğunu görüyoruz ve 0!'ı ele alırsak! bilinmeyen bir nicelik olarak ve cebirsel olarak çözdüğümüzde 3'ü görüyoruz! 0! = 3! ve böylece 0! = 1.
0 tanımının başka nedenleri de var! = 1 doğrudur, ancak yukarıdaki nedenler en açıktır. Matematikteki genel fikir, yeni fikirler ve tanımlar oluşturulduğunda, diğer matematikle tutarlı kaldıklarıdır ve sıfır faktöriyel eşittir bir tanımında tam olarak gördüğümüz şey budur.