Matematikte Çemberler ve Daireler

    Daire, uçları yuvarlak bir şekil oluşturmak için birleşen kavisli bir kenara sahip 2 boyutlu kapalı bir şekildir. 'Daire' kelimesi, küçük bir halka anlamına gelen Latince 'circulus' kelimesinden türetilmiştir. Bu sayfada birkaç daire alıştırma problemi ile daire tanımı, daire formülleri ve bir dairenin çeşitli bölümleri hakkında daha fazla bilgi edinelim.

 

Çember ve Daire nedir?

    Daire, düzlem üzerindeki sabit bir noktadan ( merkez ) sabit bir mesafede ( yarıçap ) olan bir dizi noktadan oluşan iki boyutlu bir şekildir. Sabit noktaya dairenin orijini veya merkezi denir ve noktaların orijinden olan sabit mesafesine yarıçap denir. Bir dairenin temel kısımlarını, merkezini, yarıçapını ve çapını görmek için aşağıdaki şekle bakın.

 

Bir Dairenin Parçaları

    Bir dairenin özelliklerini anlamak için bilmemiz gereken birçok parçası vardır. Bir dairenin birkaç önemli parçası aşağıda verilmiştir.

    Çevresi: Aynı zamanda bir dairenin çevresi olarak da adlandırılır ve dairenin sınırının uzunluğu olarak tanımlanabilir. 

    Dairenin yarıçapı: Yarıçap, bir dairenin merkezinden sınırındaki herhangi bir noktaya olan mesafedir. Bir dairenin sonsuz sayıda yarıçapı vardır.

    Çap: Çap, dairenin sınırındaki iki noktayı birbirine bağlayan merkezden geçen düz bir çizgidir. Dairede birden fazla çap olabileceğine dikkat etmeliyiz, ancak şunlar olmalıdır:

• Merkezden geç. 
• Düz çizgiler olun. 
• Dairenin sınırına, birbirine zıt olan iki farklı noktaya dokunun. 

    Bir Dairenin Akoru: Bir akor, çemberin sınırındaki iki farklı noktaya dokunan herhangi bir doğru parçasıdır. Bir dairedeki en uzun akor, merkezden geçen ve onu iki eşit parçaya bölen çapıdır.

    Teğet: Teğet, daireye benzersiz bir noktada dokunan ve dairenin dışında kalan bir çizgidir. 

    Sekant: Bir dairenin yayı/çevresi üzerinde iki noktayı kesen bir çizgiye sekant denir. 

    Bir Dairenin Yayı: Bir dairenin yayı, çevresinin bir parçası veya bir kısmı olan bir eğri olarak adlandırılır. 

    Bir daire içinde segmentlere ayırma: Akorun çevrelediği alana ve bir daire içindeki karşılık gelen yaya segment denir. İki tür segment vardır - küçük segment ve ana segment.

    Bir Dairenin Sektörü: Bir dairenin sektörü, iki yarıçap ile çevrelenmiş alan ve bir dairedeki karşılık gelen yay olarak tanımlanır. İki tür sektör vardır - küçük sektör ve büyük sektör.

    Bir dairenin tüm önemli kısımlarını gösteren aşağıda verilen şekle dikkat edin. 

 

Dairenin Özellikleri

    Devam edelim ve dairelerin onları diğer geometrik şekillerden farklı kılan bazı ilginç özelliklerini öğrenelim. İşte bir dairenin özelliklerinin bir listesi:

• Daire, eğri bir yüzü olan kapalı bir 2B şekildir. 
• Aynı yarıçapa sahip olan iki daire uyumlu olarak adlandırılabilir. 
• Eşit akorlar her zaman dairenin merkezinden eşit uzaklıktadır. 
• Bir akorun dik açıortayı, dairenin merkezinden geçer. 
• İki daire kesiştiğinde, kesişen noktaları birleştiren çizgi, merkez noktalarını birleştiren çizgiye dik olacaktır. 
• Çapın uç noktalarında çizilen teğetler birbirine paraleldir. 

 

Daire Formülleri

    Bir daire ile ilgili birçok formül vardır. Herhangi bir daireye ait birkaç temel daire formülünün listesini görelim.

• Bir Daire Formülünün Alanı: Bir dairenin alanı, dairenin kapladığı alan miktarını ifade eder. Tamamen yarıçapının uzunluğuna bağlıdır → Bir dairenin alanı = πr², burada 'r' yarıçap ve π = 3.14'tür.
• Bir Daire Formülünün Çevresi: Çevre, bir dairenin sınırının toplam uzunluğudur → Bir dairenin çevresi = 2πr, burada 'r' yarıçap ve π = 3.14'tür. 
• Yay Uzunluğu Formülü: Bir yay, çevrenin bir bölümüdür ( parçası ). Bir yayın uzunluğu = θ × r. Burada θ radyan cinsindendir ve 'r' yarıçaptır.
• Bir Sektör Formülünün Alanı: Bir sektör merkezde θ ( radyan cinsinden ölçülür ) bir açı yaparsa, o zaman bir dairenin sektörünün alanı = (θ × r²) ÷ 2. Burada, θ radyan cinsindendir.
• Akor Formülünün Uzunluğu: Merkezdeki akorun yaptığı açı ve yarıçapın değeri biliniyorsa hesaplanabilir. Akorun uzunluğu = 2 r sin(θ/2). Burada, θ radyan cinsindendir.
• Segment Formülünün Alanı: Bir dairenin segmenti, akorun oluşturduğu bölge ve segmentin kapsadığı karşılık gelen yaydır. Bir segmentin alanı = r²(θ - sinθ) ÷ 2. Burada, θ radyan cinsindendir.

 

Çember Teoremleri

    Açılar ve daireler hakkında bazı ilginç şeyler. 

 

Yazılı Açı

   Öncelikle, bir tanım:

   Yazılı Açı: dairenin çevresine oturan noktalardan yapılan bir açı. 

A ve C "uç noktalar" , B "tepe noktası"dır

 

Yazılı Açı Teoremleri

    Bitiş noktalarını sabit tutmak... 

    ... A° açısı,
    uç noktalar arasındaki aynı yayın neresinde olursa olsun her zaman aynıdır:

( Aynı yay teoremi tarafından gösterilen açılar olarak adlandırılır )

 

    Ve a° yazılı bir açı, 2a° merkez açısının yarısıdır. 

( Merkezdeki açı teoremi olarak adlandırılır ) 

 

    Burada deneyin ( yuvarlama nedeniyle her zaman kesin değildir ):

 

 Örnek: Açı POQ'nun boyutu nedir? ( O dairenin merkezidir )

    Açı POQ = 2 × Açı PRQ = 2 × 62° = 124°

 

Örnek: Açı CBX'in boyutu nedir?

    ADB açısı = 32° ayrıca ACB Açısına eşittir. 

    Ve ACB Açısı ayrıca XCB Açısına eşittir. 

    Yani BXC üçgeninde Açı BXC = 85° ve Açı XCB = 32° biliyoruz. 

    Şimdi bir üçgenin açılarını kullanın, 180°'ye ekleyin:

    Açı CBX + Açı BXC + Açı XCB = 180°

    Açı CBX + 85° + 32° = 180°

    Açı CBX = 63°

 

Yarım daire içindeki açı ( Thales teoremi )

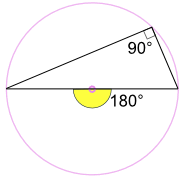
    Bir dairenin çapı boyunca yazılan bir açı her zaman bir dik açıdır:

( Uç noktalar bir dairenin çapının her iki ucudur, tepe noktası çevrenin herhangi bir yerinde olabilir. )

 

Neden? Çünkü:   90° yazılı açı, 180° merkez açının yarısıdır   ( Yukarıdaki "Merkezdeki Açı Teoremi"ni kullanarak )

 

İşe Yaramasının Bir Başka İyi Nedeni

Bir dikdörtgen yapmak için şekli 180° döndürebiliriz!    Bu bir dikdörtgendir, çünkü tüm kenarlar paraleldir ve her iki köşegen de eşittir.    Ve böylece iç açılarının tümü dik açılardır (90°).

 

Örnek: Angle BAC'nin boyutu nedir?

    Yarım Daire Teoremindeki Açı bize Açı ACB = 90° olduğunu söyler. 

    Şimdi BAC Açısını bulmak için 180°'ye eklenen bir üçgenin açılarını kullanın:

    Açı BAC + 55° + 90° = 180°

    Açı BAC = 35°

 

İşte başlıyoruz! Bu açı çevrenin neresinde olursa olsun, her zaman 90°'dir

 

Bir Dairenin Merkezini Bulma

    Bir dairenin merkezini bulmak için bu fikri kullanabiliriz:

• Dairenin çevresinin herhangi bir yerinden dik bir açı çizin, ardından iki bacağın daireye çarptığı çapı çizin
• Bunu tekrar yapın, ancak farklı bir çap için

    Çapların kesiştiği yer merkezdir! 

 

2 zıt noktadan bir daire çizmek

    Bir daire üzerinde iki zıt noktayı bildiğimizde o daireyi çizebiliriz. 

    Bu noktalara birkaç iğne veya çivi koyun ve aşağıdaki gibi bir inşaat karesi kullanın:

 

Döngüsel Dörtgen

Bir "Döngüsel" Dörtgen bir dairenin çevresindeki her köşeye sahiptir:
Döngüsel Dörtgen'in zıt açılarının toplamı 180°'dir:   A + C = 180°   B + D = 180°

 

Örnek: Angle WXY'nin boyutu nedir?

Döngüsel bir dörtgenin zıt açıları 180°'ye ulaşır

 

    Açı WZY + Açı WXY = 180°

    69° + Açı WXY = 180°

    Açı WXY = 111°

 

Teğet Açısı

    A Teğet Çizgisi sadece bir noktada bir daireye dokunur. 

    Dairenin yarıçapı ile her zaman dik bir açı oluşturur.