Matematikte Limit Nedir? Limit Ne İşe Yarar?

    Limit kelimesi Latince Limes ya da Limites‘den gelmekte olup sınır, uç nokta anlamındadır. Matematikte limit kavramından bahsedildiğinde aslında verilen bir fonksiyonun limiti anlaşılır. Sınırlar aşağıdaki gibi gösterilir:

lim ƒ(x) = L
x→a

    Yukarıdakiler, "x a'ya yaklaştıkça f(x)'in limiti L'ye eşittir" olarak okunur.

    Sınırlar, bir işlevin bir noktanın yakınındaki davranışı hakkında bilgi sağladıkları için yararlıdır. f(x) = x + 3 fonksiyonunu ele alalım. Aşağıdaki şekil, x 3'e yaklaştıkça f(x) sınırının grafiksel bir gösterimidir.

    Mavi oklar, x = 3'e yaklaştığımız yönleri gösterir ve f(x)'in x = 3'te yaklaştığı y değeri, o noktadaki sınırıdır. Bu durumda, hem sol hem de sağ taraftan 6'e yaklaştıkça fonksiyonun 3 y değerine ( kırmızı daire ile gösterilir ) yaklaştığını görürüz. Bu nedenle, x 3'e yaklaştıkça f(x) = x + 3'ün limiti 6'dır veya limit gösterimi kullanılarak:

lim(x + 3) = 6
x→3

    Bu örnekteki sınırın, x = 3'teki işlevin değerine eşit olduğuna dikkat edin. Başka bir deyişle:

ƒ(3) = 3 + 3 = 6
x→3

= lim(x + 3)
   x→3

    Bir fonksiyonun limiti ile o fonksiyonun belirli bir noktadaki değeri arasındaki fark, limitin var olan fonksiyonun değerine bağlı olmamasıdır. Böylece, bir noktada tanımsız olsa bile bir fonksiyonun limitini belirlemek mümkün olabilir. Aşağıdaki g(x) = x² - 9 / x - 3 grafik, açık daire ile gösterildiği gibi x = 3'te tanımsız olması dışında, f(x) = x + 3 ile hemen hemen aynıdır:

    Fonksiyon x = 3'te tanımsız olsa da, x 3'e yaklaştıkça limit hala 6'dır. Bu önemlidir, çünkü belirli durumlarda ( türevlerde olduğu gibi ), fonksiyonun o noktada var olup olmadığına bakılmaksızın, bir fonksiyonun bir noktadaki davranışını belirlemek isteriz. Ayrıca, fonksiyonun verilen noktada var olduğu durumlarda bile, fonksiyonun değerinin o noktadaki limitle aynı olması gerekmediğini belirtmekte fayda var.

    Yukarıdaki örnek, bir limitin grafiksel bir temsilidir. Limitleri sayısal olarak kavramsallaştırmak da mümkündür. Yukarıda kullanılan aynı işlevi göz önünde bulundurun: g(x) = x² - 9 / x - 3 . Fonksiyon x = 3'te tanımsız olmasına rağmen, limitlerin fonksiyonun ilgilenilen noktadaki değerinden etkilenmediğini biliyoruz, bu nedenle limiti belirlemek için fonksiyonu 3'e yakın ancak <>'e eşit olmayan çevreleyen x değerlerinde değerlendirebiliriz:

    Bu, grafiksel olarak belirlediğimiz şeyi, x sol veya sağ taraftan 3'e yaklaştıkça fonksiyon değerinin 6 değerine yaklaştığını doğrular. Bir limit belirlemeye yönelik sayısal yaklaşım, limit kavramını açıklamak için yararlı olsa da, genellikle diğer yöntemler kadar verimli veya etkili olmadığını belirtmekte fayda var.

Tek taraflı sınırlar

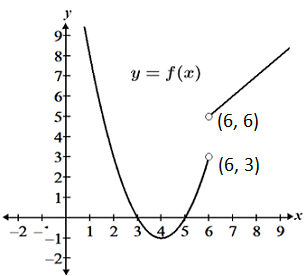
    Birkaç farklı limit türü vardır. Tipik olarak, iki taraflı bir sınır basitçe "sınır" olarak adlandırılır. Yukarıdaki örnekler iki taraflı sınırlara örnektir ( makalenin geri kalanı için sınırlar olarak anılacaktır ). Bir limitin var olmasının koşullarından biri, fonksiyonun hem sol hem de sağ taraftan yaklaştığı değerin aynı olması gerektiğidir. Sol ve sağ taraftan yaklaşılan değerler eşit olmadığında, sınır yoktur ( DNE ). Bazı durumlarda, sadece sınırın mevcut olmadığını bilmek, fonksiyonun ilgilenilen noktadaki veya çevresindeki davranışı hakkında yeterli bilgi sağlamaz. Bu durumlarda, tek taraflı sınırların incelenmesi işlev hakkında daha fazla bilgi sağlayabilir. Aşağıda gösterilen fonksiyonun grafiğini göz önünde bulundurun:

    f(x)'in limiti x = 6'da mevcut değildir, çünkü sol ve sağ el limitleri eşit değildir, ancak sol ve sağ el limitlerini değerlendirmek, fonksiyonun x = 6'da bir atlama süreksizliğine sahip olduğunu belirlememizi sağlar.

    Tek taraflı limitler, iki taraflı limitlerden yalnızca limit değeri belirlenirken dikkate alınan fonksiyonun etki alanı açısından farklılık gösterir. Bir fonksiyonun ilgili aralıklar üzerinden tanımlandığı göz önüne alındığında, solak limit, fonksiyonun değerinin bir limite, L'ye yaklaştığı bir limittir, çünkü x aralıktaki bir değere, a'ya yaklaşır. Sağ elle kullanılan bir limit de benzer şekilde tanımlanır, ancak ilgilenilen aralık a'nın sağındaki fonksiyonun alanıdır.

    Tek taraflı limitler, sırasıyla sağ ve sol el limitlerini belirtmek için + ve - sembollerinin kullanılması dışında, iki taraflı limitlerle hemen hemen aynı şekilde gösterilir:

• Sol el sınırı: 

  lim ƒ(x) = L
  x→a^—



• Sağ el sınırı: 

  lim ƒ(x) = L
  x→a⁺

    Tek taraflı sınırların olmamasının da mümkün olduğunu belirtmekte fayda var. Bu, dikey asimptotlarda veya bir fonksiyon, limiti belirli bir değere daraltmanın mümkün olmadığı bir dereceye kadar salındığında meydana gelir.

Sınırları bulma

    İkame, çarpanlara ayırma, rasyonalizasyon, sıkıştırma teoremi ve daha fazlası dahil olmak üzere bir fonksiyonun sınırını bulmak için kullanılan bir dizi farklı yöntem vardır.

Ikame

    Yerine koyma, fonksiyonun ilgilenilen noktada değerlendirilmesini içeren bir yöntemdir. Genel olarak, yalnızca fonksiyonun x = a'da tanımlandığı ve limitin fonksiyonun a'daki değerine eşit olduğu daha basit fonksiyonlar için kullanılabilir. Örneğin, x 4'e yaklaştıkça f(x) = x² - 9'un limitini bulmak istediğimizi düşünürsek, fonksiyona 4 ekler ve değerlendiririz:

lim(x² - 9) = ƒ(4) = 4² - 9 = 7
x→4

    Tüm limitlerin ikame kullanılarak hesaplanabilmesi ideal olsa da, özellikle rasyonel fonksiyonlarla çalışırken, ikamenin kullanılamadığı birçok durum vardır. Bunlar, işlev ilgilenilen noktada mevcut olmadığında veya belirsiz bir form ikame işleminden kaynaklandığında ortaya çıkar. Belirsiz formlar aşağıdakileri içerir:

0/0,∞/∞,0.∞,∞ - ∞,0⁰,1^∞,∞⁰

    Belirsiz bir form, basitçe, ikame girişiminden sonra, ifadenin sınırı belirlememiz için yeterli bilgi sağlamayan bir formda olduğu anlamına gelir. Sınırın mevcut olmaması veya sınırı başka yöntemler kullanarak belirleyebilmemiz mümkündür. Birçok belirsiz form sonsuzluğu içerirken, değeri negatif sonsuzluk veya sonsuzluk olan bir sınırın belirsiz olmadığına dikkat edin. Daha ziyade, sonsuz limit olarak adlandırılan farklı bir limit türüdür.

Faktoring

    Çarpanlara ayırma, belirsiz bir forma sahip olan bir fonksiyonun limitini değerlendirmek için kullanılabilecek yöntemlerden biridir. Özellikle, pay ve paydadaki çarpanlara ayrılmış terimlerin birbirini ortadan kaldırdığı ve fonksiyonun artık belirsiz bir form olmamasına neden olduğu fonksiyonlar için kullanılabilir.

    Örnek

lim x³ - 27 / x - 3
x→3

    İfade çarpanlarının payı (x - 3)(x² + 3x + 9), bu nedenle sınır şu şekilde basitleştirilir:

lim (x - 3) (x² + 3x + 9) / (x - 3)
x→3

= lim(x² + 3x + 9)
   x→3

    Sınır daha sonra şu şekilde hesaplanabilir:

lim(x² + 3x + 9) = 3² + 3(3) + 9 = 27
x→3

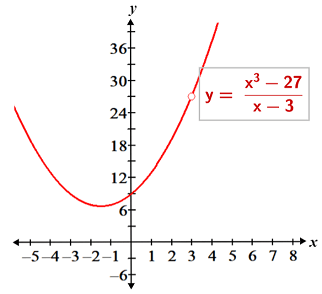
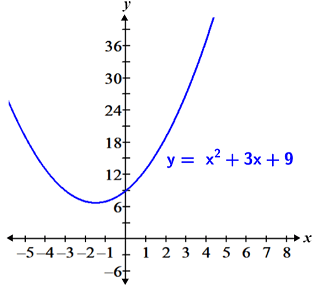
    Bu yöntemin çalışmasının nedeni, orijinal ifadenin ve basitleştirilmiş ifadenin yalnızca x = 3'te ( orijinal ifadenin tanımsız olduğu durumlarda ) farklılık göstermesi ve bu farkın x = 3'teki sınırın değerini etkilememesidir. Bu, aşağıda gösterilen grafiklerde belirgindir:

Rasyonalizasyon

    Rasyonalizasyon, belirsiz bir formun sınırını bulmak için kullanılabilecek başka bir yöntemdir. Rasyonalizasyon, işlevi basitleştirmek için bir ifadenin eşleniği ile çarpılmasını ifade eder. Rasyonalizasyonun amacı, faktoringinkiyle aynıdır, ikisi arasındaki fark, yöntemlerin basitleştirmek için kullanılabileceği ifade türleridir.

Örnek

lim √x + 4 - 2 / x
x→0

    İfadenin payını ve paydasını payın eşleniği ile çarparak payı rasyonelleştirin:

lim √ x + 4 - 2 / x
x→0

= (lim √ x + 4 - 2 / x)(√ x + 4 - 2 / √ x + 4 - 2)
   x→0

= lim ( (x + 4) - 4 / x(√ x + 4 + 2) )
   x→0

= lim ( (x / x(√ x + 4 + 2) )
   x→0

= lim ( 1 / √ x + 4 + 2 )
   x→0

    Sınır daha sonra aşağıdaki gibi hesaplanabilir:

lim ( 1 / √x + 4 + 2 ) = 1 / √0 + 4 + 2 = 1 / 4
x→0

Sıkma teoremi

    Sandviç teoremi veya kıstırma teoremi olarak da adlandırılan sıkma teoremi, bir limit bulmak için kullanılan başka bir yöntemdir. Faktoring ve rasyonalizasyon gibi yöntemlerin işe yaramadığı bazı durumlarda kullanılabilir. Sıkma teoremi şu şekilde tanımlanır:

    f(x), g(x) ve h(x) öyle fonksiyonlar olsun ki, a'yı içeren bir aralıktaki tüm x değerleri için, belki a'da hariç,

g(x) ≤ ƒ(x) ≤ h(x)

    Ek olarak, varsayalım ki

lim g(x)
x→a

= lim h(x) = L
   x→a

    Sonra:

lim ƒ(x) = L
x→a

    Başka bir deyişle, f(x), g(x) ve h(x) arasında sıkıştırıldığından, g(x) ve h(x) a'da aynı limite sahipse, f(x)'in de aynı limite sahip olması gerekir.

    Sıkıştırma teoremini kullanmak için, g(x) ve h(x) arasında sıkıştığından emin olabileceğimiz f(x)'e yeterince benzer fonksiyonlar bulmamız gerekir. Ayrıca g(x) ve h(x) limitlerinin hesaplanması daha kolay olacak şekilde fonksiyonlar seçmek istiyoruz.

    Örnek

lim x³ cos (1/x³)
x→0

    Bu durumda sıkma teoremini uygulamak için aşağıdaki gerçeği kullanırız:

-1 ≤ cos(x) ≤ 1

    Bu gerçek, x = 0'da tanımsız olmasına rağmen fonksiyonumuz için geçerlidir, çünkü fonksiyonun belirli bir noktada tanımsız olmasının o noktadaki limiti etkilemediğini biliyoruz. Böyle:

-1 ≤ cos(1/x³) ≤ 1

    Daha sonra, limitini kolayca hesaplayabileceğimiz iki fonksiyon arasında f(x) elde etmek için eşitsizliği x³ ile çarpabiliriz:

-x³ ≤ x³cos(1/x³) ≤ x³

    Beri

lim(-x³)
x→0

= lim(x³) = 0
   x→0

    Şu sonuca varabiliriz:

lim x³ cos (1/x³) = 0
x→0

    Limitleri değerlendirmenin başka yolları da olduğunu unutmayın, ancak bunlar türevlerin kullanımını içermeyen en yaygın yollardan bazılarıdır. Türevleri içeren zor limitleri hesaplama yöntemi için L'Hopital kuralı kullanılır.

Limit Ne İşe Yarar?

    Doğrudan matematikle ilgisi olmayan birine “Günlük yaşamda limit ne işine yarayacak?” diye sorulursa; buna cevap vermek pek kolay değil. Hatta doğrudan hiçbir işine yaramayacak desek çok da yanılmış olmayız. Tabi büyük resme odaklanırsak bazı şeyler değişecektir.

    Türev ve integral kavramlarıyla birlikte değişimin matematiğine de sahip olmaktayız. Bu sayede durağan yapılarla ilgilenen matematik bir anda evrenin her yerinde söz sahibi olduğunu göstermiştir. Limitin çok değerli bu iki kavramın tanımlarında ( köklerinde ) yer alması ise son derece mühimdir.

    Asla değişmeyecek bir şey, dünyanın sürekli değiştiği gerçeğidir. Türev ve integral değişimin matematiğidir. Dolayısıyla değişimin olduğu her yerde bu iki kavram kendisini gösterecektir. Bunların olduğu her yerde de aslında limit karşımıza çıkacaktır.

    Türev, bir niceliğin başka bir niceliğe göre değişimidir. Örneğin yolun zamana bağlı değişimi olan hız veya hızın zamana bağlı değişimi olan ivme türev kavramı ile tanımlanır. Genellikle türevin tersi olarak bilinen integral kavramı ise belirli bir aralıktaki toplam değişimi belirtir.

    Newton ve Leibniz’le başlayan türev ve integralin sağlam bir zemine oturtulması sürecinde limit kavramsal olarak ortaya çıkmıştır. Sonuç olarak limit kavramının matematikte tek başına fazla bir anlamı yoktur. Ancak türev ve integral hesaplamalarında süreklilik, bir fonksiyonun türevi ve bir fonksiyonun belirli integrali gibi önemli sonuçları elde etmemize yarayacaktır. Bu nedenle de matematiğin kalbinde yer alır.