Fonksiyon Nedir ve Ne İşe Yarar?
Fonksiyon Nedir ve Ne İşe Yarar?
- BİLİM ve TEKNOLOJİ
- Sun, 29 Jan 2023 23:05:55
- Sun, 29 Jan 2023 23:05:55
İşlev ( Fonksiyon ) kelimesi ne anlama geliyor? İşlev kelimesiyle, kişinin oynaması gereken sorumluluğu veya rolü anlıyoruz. Bitki yapraklarının işlevi nedir-bitki için yiyecek hazırlamak ve saklamak? Bitki köklerinin işlevi nedir? Suyu ve diğer besinleri yerden emerek bitkilere verirler ve dik durmalarına yardımcı olurlar. Herkesin farklı işlevleri olduğunu söyleyebilir miyiz? Matematikteki bazı işlev türleri hakkında bilgi edelim!
İşlevler ( Fonksiyonlar )
Bir işlevi, A kümesinin her bir öğesini B kümesinin yalnızca bir öğesiyle eşleştiren özel bir ilişki olarak tanımlayabiliriz. Hem A hem de B kümeleri boş olmamalıdır. Bir işlev, belirli bir girdi için belirli bir çıktıyı tanımlar. Bu nedenle, f: A → B, a ∈ A için benzersiz bir b element B öğesi olacak şekilde bir işlevdir, öyle ki (a, b) ∈ f
İşlev ( Fonksiyon ) Türleri
Bire Bir İşlev
Bir fonksiyon f: A → B, A'nın her bir elemanı için ayrı bir B elemanı varsa Bire Birdir. Enjekte Edici olarak da bilinir. Bir 1 ∈ A ve bir 2 if B, f'nin f: A → B olarak tanımlanıp tanımlanmadığını düşünün, öyle ki f (a1) = f (a2)
Bir Fonksiyona Çok
A'nın iki veya daha fazla öğesini B kümesinin aynı öğesiyle eşleştiren bir işlevdir. A'nın iki veya daha fazla öğesi B'de aynı görüntüye sahiptir.
İşlev Üzerine
B kümesinin her öğesinin A kümesinde ön görüntü( ler ) olduğu bir işlev varsa, İşlev Üzerindedir. Onto ayrıca Surjektif İşlev olarak da adlandırılır.
Bire Bir ve İşlev Üzerine
Bir fonksiyon, f Bire Birdir ve Üzerine veya Bijektif eğer fonksiyon f hem Bire Birdir hem de Üzerine işlevdir. Başka bir deyişle, f işlevi, A'nın her bir öğesini ayrı bir B öğesiyle ilişkilendirir ve B'nin her öğesinin A'da bir ön görüntüsü vardır.
Diğer İşlev Türleri
Bir işlev, koordinat olarak tüm x ve f(x) çiftlerinden oluşan bir kümeden başka bir şey olmayan grafiğiyle benzersiz bir şekilde temsil edilir. Fonksiyon türleri ve grafikleri hakkında daha fazla bilgi edinmeye hazırlanalım.
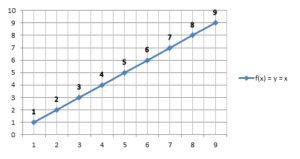
Kimlik İşlevi
R gerçek sayılar kümesi olsun. F: R→R işlevi, x ∈ R için f(x) = y = x olarak tanımlanırsa, işlev Kimlik işlevi olarak bilinir. Grafik her zaman düz bir çizgidir ve orijinden geçer.
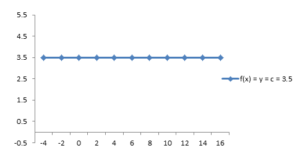
Sabit Fonksiyon
F: R→R işlevi f(x) = y = c olarak tanımlanırsa, x ∈ R ve c için R'de bir sabittir, o zaman bu işlev Sabit işlev olarak bilinir. F fonksiyonunun alanı R'dir ve aralığı sabittir, c. Bir grafik çizerek x eksenine paralel düz bir çizgi buluruz.
Polinom Fonksiyonu
Bir polinom işlevi şu şekilde tanımlanır: y =a0+ a1x + a2x2+ ... + anxn, burada n negatif olmayan bir tamsayıdır ve a0, a1, a2,..., n ∈ R. İfadedeki en yüksek güç, polinom fonksiyonu. Polinom fonksiyonları derecelerine göre daha da sınıflandırılır:
- Sabit Fonksiyon: Derece sıfır ise, polinom fonksiyonu sabit bir fonksiyondur ( yukarıda açıklanmıştır ).
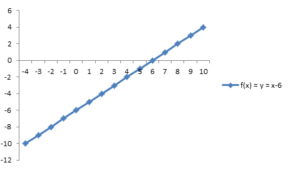
- Doğrusal Fonksiyon: Birinci dereceden polinom fonksiyonu. Örneğin, y = x + 1 veya y = x veya y = 2x - 5 vb. Dikkate alındığında, y = x – 6. Etki alanı ve aralık R'dir. Grafik her zaman düz bir çizgidir.
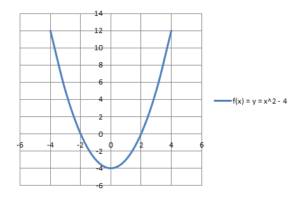
İkinci Dereceden Fonksiyon: Polinom fonksiyonunun derecesi iki ise, o zaman ikinci dereceden bir fonksiyondur. F(x) = ax2+ bx + c olarak ifade edilir, burada a ≠ 0 ve a, b, c sabittir ve x bir değişkendir. Etki alanı ve aralık R'dir. İkinci dereceden bir fonksiyonun grafiksel gösterimi, f(x) = x2-4
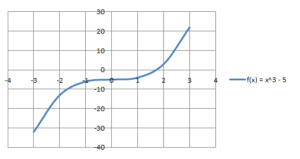
- Kübik Fonksiyon: Kübik bir polinom fonksiyonu, üçüncü dereceden bir polinomdur ve f(x) = ax3+ bx2+ cx +d ile gösterilebilir, burada a ≠ 0 ve a, b, c ve d sabittir ve x bir değişkendir. F(x) = y = x3– 5 için grafik. Etki alanı ve aralık R'dir.
Rasyonel İşlev
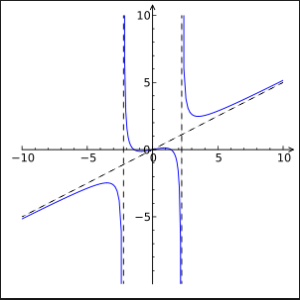
Rasyonel bir fonksiyon, rasyonel bir kesirle temsil edilebilen herhangi bir fonksiyondur, örneğin, f(x)/g(x), pay, f(x) ve payda, g(x), x'in polinom fonksiyonlarıdır, burada g (x) ≠ 0. Bir fonksiyonun f: R → R tanımlanmasına izin verin, f(x) = 1/(x + 2.5). Grafik gösterimi asimptotları, eksen çizgilerine dokunuyor gibi görünen eğrileri gösterir.
Modül Fonksiyonu
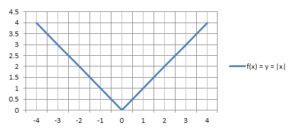
Herhangi bir sayının mutlak değeri, c |c / şeklinde temsil edilir. Herhangi bir işlev f: R→ R, f(x) = |x / ile tanımlanırsa, Modül İşlevi olarak bilinir. X'in negatif olmayan her değeri için, f(x) = x ve x'in her negatif değeri için, f(x) = -x, yani.,
f (x) = {x, eğer x ≥ 0 ise; - x, eğer x < 0 ise.
Grafiği, alanın ve aralığın R olduğu yer olarak verilir.
Signum İşlevi
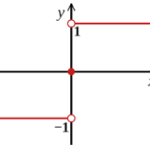
Bir fonksiyon f: R→ R tarafından tanımlanır
f (x) = { 1, eğer x > 0 ise; 0, eğer x = 0 ise; -1, eğer x < 0 ise
Signum veya sign işlevi, gerçek sayının işaretini çıkarır ve adım işlevi olarak da bilinir.
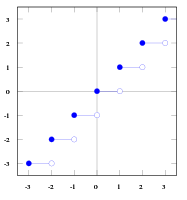
En Büyük Tamsayı İşlevi
Bir işlev f: R→ R, f(x) = [x], x ∈ X ile tanımlanırsa, sayıdan küçük tamsayıya gerçek sayıya yuvarlanır. Verilen aralığın (k, k+1) şeklinde olduğunu varsayalım, en büyük tamsayı fonksiyonunun değeri bir tamsayı olan k'dir. Örneğin: [-21] = 21, [5.12] = 5. Grafik gösterimi şöyledir
Sizin için Çözülmüş Örnek
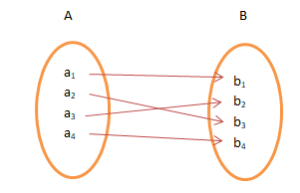
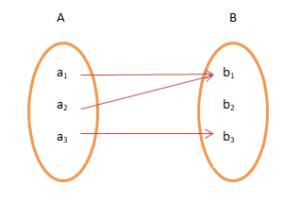
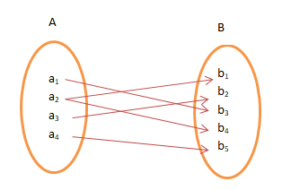
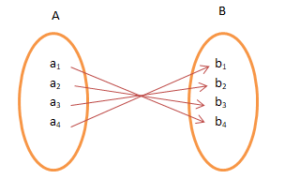
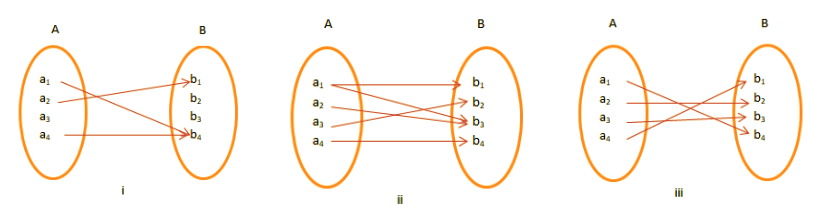
Soru 1: Aşağıdakilerden hangisi bir işlevdir?
Cevap: Şekil ( ııı ) bir fonksiyon örneğidir. Şekil ( ıı ) ' de, verilen işlev, A'nın her bir öğesini B'ninkiyle eşleştirdiğinden, verilen işlev, A'nın bir öğesini B'nin iki öğesiyle ( bire çok ) eşleştirir. Şekil ( i ), işlev tanımının ihlalidir. Verilen işlev, A'nın her öğesini eşlemez.
Soru 2: İşlev ile ne kastedilmektedir ve türleri nelerdir?
Cevap: Bir işlev, bir kümenin her bir öğesini başka bir kümeye ait yalnızca bir öğeyle eşleştiren özel bir ilişkiyi ifade eder. Çeşitli işlev türleri aşağıdaki gibidir:
- Bir fonksiyona çok
- Bire bir işlev
- İşlev üzerine
- Bir ve fonksiyon üzerine
- Sabit fonksiyon
- Kimlik işlevi
- İkinci dereceden fonksiyon
- Polinom fonksiyonu
- Modül fonksiyonu
- Rasyonel işlev
- Signum işlevi
- En büyük tamsayı işlevi
Soru 3: Bir fonksiyonun çalışması nasıl gerçekleşir?
Cevap: Bir işlev, her x için y için yalnızca bir yanıt sağlayan bir denklemi ifade eder. Belirli bir türdeki her girişe bir işlev tarafından tam olarak bir çıktı atanması vardır.
Soru 4: Bir fonksiyonun bir fonksiyon olup olmadığı nasıl belirlenebilir?
Cevap: Bir denklemin y için çözerek bir fonksiyon olup olmadığı belirlenebilir. Bir denklem ve x için belirli bir değer olması durumunda, o belirli x değeri için yalnızca bir karşılık gelen y değeri olacaktır.
Soru 5: Bir parabolün bir fonksiyon olduğunu söyleyebilir miyiz?
Cevap: Sadece aşağı veya yukarı açılan paraboller fonksiyonlardır.